ホームスクーラーでギフテッドのＲ君の夢中な色々

数学や物理の定理のキレイさ、スゴさに基づいてランキングを作りました。第十位からご紹介！

第八位：モーリーの定理
『任意の三角形について、各頂点から内角の三等分線を引くと、各辺に近い線同士の交点により構成される三角形は正三角形である。』
つまり、どんな三角形でも内角の三等分線を引くと、真ん中に正三角形が出来るという定理です。使い道はあんまりないですが、かなり強烈な定理です。以下に、三角形でこの定理が成り立つことを確認した画像を示します。三角形EFGが正三角形になってます！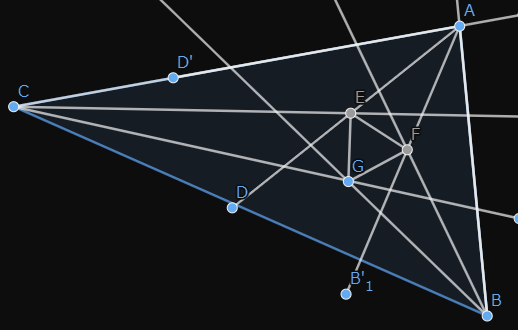




第七位：グルサの定理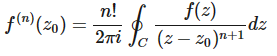

この式が成り立つことを示す定理です。ただし、zは複素変数です。
つまり、複素関数のn階微分は積分として表せるということです。
私は、この定理を見たときびっくりしました。なぜなら、反対の操作である微分と積分がイコールで結ばれているのですから。でも、今はそのような意外性も含めて、いい定理だなと思っています。さらに、この定理は利便性も高いです。

第六位：チェビシェフの不等式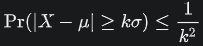

任意の確率分布についてこの式が成り立つというもの。ただし、μは平均(期待値)、σは標準偏差を表す。
すなわち、どのような確率分布だったとしても、平均から標準偏差のn倍以上離れた値は全体のn^(-2)以下であるということ。
しかし、この『任意の確率分布について』なにか述べてくれるのが頼もしいですねぇ。

第五位：二項定理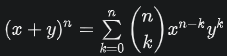

この式が成り立つとする定理です、
すなわち、(x+y)^rを展開すると、各項の係数は『組み合わせ』で表されるということ。
この定理がすごいのは、展開した時の一つの項の係数の大きさだけが知りたいとき、展開しなくてもこの定理から一発で分かるという点です。高校の教科書にも必ず載っている有名な定理。やっぱりキレイです。特に私は上に挙げた総和記号でまとめてある形が好きです。

第四位：カルダノの公式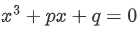

の解は、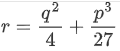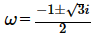
，
とおくと、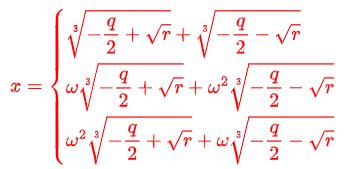

の三つで表されるという公式です。
この公式は、何度見ても衝撃的です。でも手計算でやるとなると計算間違いする感じしかしませんので、実用ではないと言わざるを得ません。また、簡単な複素数で表されるのに三乗根でくくられてしまっていて、うまく整理できなかったりすることもあるので、そこも悲しいポイントです。でも、Tシャツの柄にするには最高ですね（笑）

第三位：マクスウェルの方程式
古典電磁気学の基本性質を四つにまとめたものです。積分形と微分形があるので、どちらも示します。
積分形：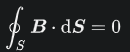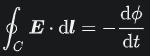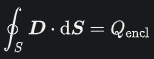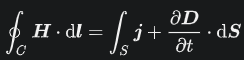




微分形：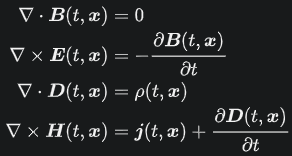

この方程式は上から順番に、磁束保存の方程式、ファラデー・マクスウェルの方程式、マクスウェル・ガウスの方程式、マクスウェル・アンペールの方程式と呼ばれていて、電磁気学の分野においては、四則演算（？）のようによく使うものです。私個人としてもかなり好きな式です。

第二位：オイラーの等式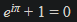

という式です。では、登場する数を紹介して置きます。
・自然対数の底e
・円周率π
・虚数i
・乗法の単位元1
・加法の単位元0
基本的な数が勢ぞろい、それが綺麗に纏まっている奇跡の式です。
何度見ても綺麗ですね。

第一位：区分求積法の定義式
関数f(x)が開区間[a,b]で連続かつ微分可能な時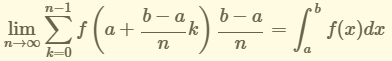

が成立するというものです。
これは、グラフの下の面積を無限に縦割りして、それの総和を取るとこで積分を表すというものです。でも、私はこの式が『積分（面積求値としての側面）の定義式』だと思っています。人生で初めて式を見て感動するという体験をさせてくれた式です。
数学のかっこいい式といえば...と頭に思い浮かべてみると、必ずこの式が最初に浮かびます。
普通、数学の美しさランキングだと、オイラーの等式が一位のようですが、私の中では区分求積法の定義式が一位です。

以上、数学＆物理の定理ランキングでした。
ここまで御読みくださりありがとうございます！