反交換律 → 反強磁性?[2015年11月08日Cold atomic gases原子ガス --- condensed matter physics（物性物理 ）[5]("spin liquid ordering"極低温？のなかでの量子スピン液体状態は、反強磁性相互作用？・・「高温超伝導」 （高温という語は、通常は人間が「熱い」と感じるほど温度が高いことを表すが、高温超伝導における高温とは、従来の超伝導体と比較すると高温である−200〜−100 ℃程度を指す）・・・ベドノルツとミューラー（ミュラー）が、La-Ba-Cu-O系において1986年に発見したことから始まり、その後続々と発見された転移温度が液体窒素温度（−195.8 ℃, 77 K）を越える一連の銅酸化物高温超伝導物質と、その超伝導現象のことを指す場合が多い. 高温超伝導を示す物質のことを高温超伝導体という. 銅酸化物であるものは銅酸化物高温超伝導体という[1987年のノーベル物理学賞を受賞]. / (ケルビン→冷却原子気体→ボース＝アインシュタイン凝縮（レーザー冷却）→量子コンピュータの実験(この発見に類する？応用の一部？？？) ), 2015年11月10日ultracold atom[冷却原子気体] --- condensed matter physics（物性物理 ）[6](絶対零度では熱によるゆらぎは抑制されており、またエントロピーの変化も期待できないため、不確定性原理による「量子ゆらぎ」により、量子相転移が起こりえると考えられる様になってきました. 特定の物質？に・・ある温度で反強磁性などの秩序を持つ相への相転移が起こるとします. その物質に『圧力や磁場をかけたり、化学組成を少し変えたりする（制御パラメータとよばれます）』ことで、相転移温度を減少させることが可能です(びみょうなさの温度減???, しかし、このびじゃくな差の温度減？？が新発見!! でおおきい !?!?!, → 〔新・技術!? のたんじょう〕!?!,?? ) ) etc.. ]
An n-ary operation is anticommutative if swapping the order of any two arguments negates the result. For example, a binary operation2項演算[ブール演算 ] ∗ is anti-commutative (with respect to addition) if for all x and y,
x ∗ y = −(y ∗ x).
More formally, a map ∗ : A ^n → G from the ''set of all n-tuples "「順序組 」 (有限な長さの列を言う. 特に非負整数 n に対して、n 個の要素や成分などとも呼ばれる元あるいは対象を順番に並べたもは n-組 (n-tuple) . 2-組（あるいは二つ組, couple）は特に対 (pair) または「ordered pair順序対(0-組はただ一つ存在して「何も並べないこと」を意味するが、文脈によりそれは空集合や、空列や、空リストなどと呼ばれる. 1-組（あるいは一つ組）は定義により、ただ一つの元からなる集合、ただ一つの項からなる列、ただ一つの点からなる空間などであって、それはそのそれぞれのただ一つの要素であるところの元、項、点などとは厳密には異なるが、にも拘らず多くの場合においてその唯一の要素と同一視して、あるいはそれら要素自身を指す意味で用いられる. 小さい n に対する n-組はしばしば、3-組を「三つ組」(triple)、4-組を「四つ組」(quadruple) などのように呼ぶこともある. ) 」という特別な呼称を持つ. ) of elements in a set A (where n is a non-negative integer) to a group G is anticommutative with respect to the additively denoted group operation if and only ifx _1 ∗ x _2 ∗ ⋯ ∗ x _n = sgn ( σ ) ( x _σ ( 1 ) ∗ x _σ ( 2 ) ∗ ・・・ ∗ x _σ ( n ) ) ∀ x = ( x _1 , x _2 , … , x _n ) ∈ A _n
where σ : ( n ) → ( n ) is an '''arbitrary permutation "" of the set (n) of the first n positive integers and s g n ( σ ) is its sign. This "equality expresses '' the following concept:
・the value of the operation on some fixed ordered n-tuple is unchanged when applying any even permutation置換 to the arguments, and
・the value of the operation is the 'additive inverse "加法に関する逆元(~ For every integer a, there is an integer b such that a + b = b + a = 0. The integer b is called the inverse element of the integer a and is denoted −a. .. .,,.. The integers, together with the operation +, form a mathematical object belonging to a broad class sharing similar structural aspects. To appropriately understand these structures as a collectiveこれは? 「行列(集合的協約?(集合協約的)?? ) 」 をいみする ?!?, the following abstract definition is developed.（a,b はもちろん「行列 」かんぜんな =0 になるには・むずかしい しかし・だから・ふくざつせいが・うまれるし？・「複素数」[超越数,, ] をおりこんだ・・むげんへの・ちょうせんが・かのうと・なる？？？, ） ) of this value, whenver an odd permutation is applied to the arguments. The need for the existence of this additive inverse element is the main reason for requiring the codomain G of the operation "∗ " to be at least a group.
Particularly important is the case n = 2. A binary operation ∗ : A × A → G is anticommutative if and only if(～の場合に限り[iff ] ) (2進[鍼?/]?法 では 逆[^減法「加法的逆運算(ちゅうごく語ではこうかく??)」？] の交換子 がなりたつ ?? と「人工知能 'computerｓ 」' はいっておられる ???, )
x _1 ∗ x _2 = − ( x _2 ∗ x _1 ) ∀ ( x _1 , x _2 ) ∈ A × A
This means that x_1 ∗ x_2 is the additive inverse of the element x_2 ∗ x_1 in G
by Wikipedia
(原子核を安定化する引力（強い相互作用）を媒介するボソンの一種「パイ中間子(パイ粒子、パイオン（Pion）) 」・・・安定化につながるいんし ??? ・・反交換関係をつくるのは[律? ]をはかり中間的な安定をはかる・ため ？(ちょっと？うんどうてきなもの[ようそ?]?? を・くわえる・ひつようが・ある ??? )？？, σ^{μν} = γ^{μ}γ^{ν} ? γ^{ν}γ^{μ} <Physical structure---/wiki/Gamma matrices > γ は「行列」・・・、このけいさんで・あう( 「対合((~ 自分自身をその逆として持つ写像である.
f ^{− 1} ( x ) = f ( x ) , for any x .
これは空間上の変換であって、二回繰り返すと恒等変換となる（元に戻る）という性質
λ ( λ ( x ) ) = x , for any x
を持つものと言ってもよい. ただし、それ自身が恒等変換となるものは通常は除いて考える. またこれは変換群に属する位数 2 の元
σ which satisfies σ ^2 = i d e n t i t y
を指すと言っても同じことであり、それを理由に一般の群（抽象群）においても位数 2 の元を対合と呼ぶことがある.
・平面上の任意の点 x を、ある直線 l に関して対称な点 φ(x) に写す操作（鏡映）φ は、明らかに φ(φ(x)) = x を満たすから φ は平面上の対合である.
・集合 A に対し、普遍集合 S において A の補集合 A^c をとる操作は、(A^c)^c = A を満たすから、この変換は S の冪集合における対合である.
・複素数 z に対しその共役複素数 z^* をとる複素数体 C 上の変換は、 (z^*)^* = z を満たすから対合である.
<例ーー/wiki/対合 >
群 G が与えられ、その上の写像 I: G → G が対合であって、次の関係
( g h ) ^I = h ^I g ^I , for any g , h ∈ G
を満たすとき、対合 I は G の群構造と両立するといい、組 (G, I) を対合付きの群と呼ぶ. 群の逆元をとる演算
g ↦ g ^{− 1}
は g, h を G の元とすれば
( g ^{− 1} ) ^{− 1} = g ,
( g h ) ^{− 1} = h ^{− 1} ・ g ^{− 1}
を満たすので、これは群が標準的に持つ群構造と両立する対合である.
また、環 R とその上に対合 "* ": R → R で
( r + s ) ^∗ = r ^∗ + s ^∗ , for any r , s ∈ R ,
( r s ) ^∗ = s ^∗ r ^∗ , for any r , s ∈ R ,
1 _R ^∗ = 1 _R
を満たすものの組 (R, "* " ) として対合付き環の概念が得られる. もっと一般に必ずしも可換でないものを含む二項演算（と単項演算、0項演算）のみからなる代数系 A にその上の対合 σ が存在するとき、σ が A からその逆代数系 A^{opp} への準同型となる（つまり、二項演算の順番を逆にし、単項、0 項演算と可換となる）とき、代数系 A の構造と対合 σ は両立するといい、組 (A, σ) を「対合つき代数系 」 と呼ぶ. たとえば、n 次全行列環 Mn(K) (K は可換環あるいは体)に、行列を転置させる写像 t を考えたとき、x, y を行列、λ をスカラーとすると
^t ( ^t x ) = x ,
^t ( x + y ) = ^t x + ^t y
^t ( x y ) = ^t y ・ ^t x
^t ( λ x ) = λ ^t x
が満たされるので、(M_n(K), t) は対合つき多元環である.
体 L が対合となる自己同型 σ を持つとき、σ の固定体を F とすると、拡大 L/F は二次拡大である. <対合つき代数系ーー/wiki/対合 >
鏡映群、コクセター群[2016年02月20日transposition互換 --- symmetric group 対称群, 2017年05月21日ミンコフスキー空間・ローレンツ変換 etc .. → Influence on later work---/wiki/エルランゲン・プログラム(;affine geometry放射幾何学？？ ), 2017年06月24日definitions and first examples---root systemルート系, 2018年01月28日gauge invariant QCD Lagrangian (場の理論)[Theory]---quantum chromodynamics(量子色力学)[21], 2018年02月17日related classifications(1)---Dynkin diagramディンキン図形(ミラー対称性_(弦理論）-wiki ??? ・・ けっきょくは？・(代数学における？・) びぶんせきぶん・けいさん(GPS?におうよう？? diagram をworm する？,・ )がだいじ ?!?!?, ), definition---Coxeter groupコクセター群[1]20180220, efinition---Coxeter groupコクセター群[2]20180302 etc... ] は、（位数 2 の元という意味での）対合からなる生成系を持つ群である.
<対合で生成される群ーー/wiki/対合 >
) ) 」 （?適合??）する？)?? 「行列」をコンピューターは・虱潰[しらみつぶ ] し にさがしてくれる・だから・「制御. 」の精度?!, はかぎりなく・あがっていく(向上していく??)? )
<関連, >
自己同型 α に加えて、クリフォード代数の解析(→ 原子核を安定化する引力?? )において重要な役割を果たす 2 つの反自己同型が存在する. テンソル代数 T(V) はすべての積の順序を逆にする反自己同型とともに来ることを思い出そう：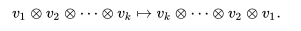
<figure >
イデアル I_Q はこの反転の下で不変なので、この演算は Cℓ(V, Q) の反自己同型に降り、転置 (transpose) あるいは反転 (reversal) 演算と呼ばれ、^t x (^t は角度?? ) によって表記される. この反転は反自己同型である： ^t(xy) = ^t y ・^tx. 転置演算は Z_2-次数付けを全く使わないので2つ目の反自己同型を α と転置を合成することによって定義する. この演算をクリフォード共役 (Clifford conjugation) と呼び x と表記する
x ¯ = α ( ^t x ) = ^t ( α ( x ) ) .
2 つの反自己同型のうち転置はより基本的である.
これらの演算は全て対合であることに注意しよう. それらは Z-次数付けにおいて pure な元上 ±1 として作用することを示すことができる. 実際、すべての 3 つの演算は次数 modulo 4 にしか依らない. つまり、x が pure で次数 k であれば、α ( x ) = ± x ^t x = ± x x ¯ = ± x
ただし符号は以下の表によって与えられる：
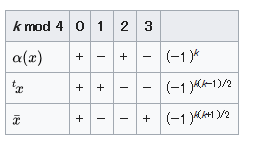<figure >
<反自己同型写像(性質 )ーー/wiki/クリフォード代数 >
2015年04月06日随伴関手Adjoint functors
幾何ではかんぺきでも・・代数的には？？・・・それをおいつづけているのは・・computing ??? （いったん、・・無理数的要素が・・計算積のなかにはいると・・逆戻りできない・・＝の計算式ができあがる？！・・・それを代数化し・・computerのなかにおりこむには・・---随伴行列的組入れ・・？！？・・・すうがくてきには・・環論とどうようの無限のどうしようもない誤差的なものができてしまうような・・？？ ・・・しかし・・むりすうは・・随伴させると・・ゆうりすうになる？?？ ）)
2015年04月07日tensor product テンソル積
（ちがった構成要素？？・・・対象を巨視的に捉え、空間的に微分可能な連続体に理想化し、物体内部の各点における力学的な関係式を元に、変形・流動、波動の伝播、エネルギーの変換等を・・・制御目的で・・これを・・基本となる演算として・・けいさんしようとする・・？！？・・多重線型代数・クリフォード代数・四元数・「回転行列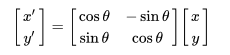
<2次元の回転行列、3次元の回転行列ーー/wiki/rotation matrix回転行列 > 」 などなどとともに・・？？？ bilinear operation双線型作用[演算]？. ）
クリフォード代数
2016年08月09日Pauli matricesパウリ行列
quaternion;四元数
複素数を拡張した数体系である. 四元数についての最初の記述は、1843年にアイルランドの数学者ウィリアム・ローワン・ハミルトンによってなされ、三次元空間の力学に応用された. 四元数の特徴は、二つの四元数の積が非可換となることである. ハミルトンは、四元数を三次元空間内の二つの有向直線の商として定義した. これは二つのベクトルの商と言っても同じである. 四元数をスカラーと三次元のベクトルとの和として表すこともできる. 四元数は純粋数学のみならず応用数学、特に3Dグラフィクスやコンピュータビジョンにおいて三次元での回転の計算でも用いられる. これはオイラー角や回転行列あるいはそれらに代わる道具などとともに、必要に応じて利用される
2017年10月23日software implementation---incomplete beta function 不完全ベータ関数
(丸め誤差を許容して計算を行なってもけいさんせいどをあげることがかのうとなった ?!? 計算誤差を綿密?に人工的に修正した？・・固定的な数論的計算を挿入する?? ことによって、・計算精度をたかめている ?!?!,? → ('computer'ならバグ?のようなものができてしまう？！,(しょせん？行列[式]?!によりつじつまあわせ(代数的-?!? ))？ )) ・・なのかもしれない？？？？,？ )
また，数式処理システムに向けた計算アルゴリズムを研究する分野も数式処理（あるいは computer algebra の直訳として計算機代数）と呼ぶ）
.
H.Nakao@
