Let C = { e _1 , … , e _n } be a basis for V. Define the n × n matrix A by A _{i j} = B ( e _i , e _j ) . The matrix A is a '''symmetric matrix「対称行列 」 ""<~ In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if
A = A ^T .
Because equal matrices have equal dimensions, only square matrices can be symmetric.
The entries of a symmetric matrix are symmetric with respect to the main diagonal「主対角線(行列の一番左上から一番右下にかけての対角線. ) 」. So if the entries are
written as A = (a_{ij} ), then a_{ij} = a{ji}, for all indices i and j.
（ ?適合(involution対合[definition---anticommutativity反交換子関係[律? ]20180312((2進[鍼?/]?法 では 逆[^減法「加法的逆運算」？] の交換子 がなりたつ ?? ~ 自分自身をその逆として持つ写像である.
f ^{- 1} ( x ) = f ( x ) , for any x .
これは空間上の変換であって、二回繰り返すと恒等変換となる（元に戻る）という性質
λ ( λ ( x ) ) = x , for any x
を持つものと言ってもよい. ただし、それ自身が恒等変換となるものは通常は除いて考える. またこれは変換群に属する位数 2 の元
σ which satisfies σ ^2 = i d e n t i t y
を指すと言っても同じことであり、それを理由に一般の群（抽象群）においても位数 2 の元を対合と呼ぶことがある.
・平面上の任意の点 x を、ある直線 l に関して対称な点 φ(x) に写す操作（鏡映）φ は、明らかに φ(φ(x)) = x を満たすから φ は平面上の対合である.
・集合 A に対し、普遍集合 S において A の補集合 A^c をとる操作は、(A^c)^c = A を満たすから、この変換は S の冪集合における対合である.
・複素数 z に対しその共役複素数 z* をとる複素数体 C 上の変換は、 (z^*)^* = z を満たすから対合である.
<例ーー/wiki/対合 >) etc? ] で生成される)??）する？)?? 「行列」をコンピューターは・虱潰[しらみつぶ ] しにさがしてくれる.
The following 3 × 3 matrix is symmetric:
[ 1 7 3 7 4 − 5 3 − 5 6 ]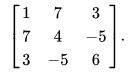 
<figure > .
Every square ''diagonal matrix is symmetric '", since all off-diagonal elements are zero.
Similarly in characteristic「標数 」[2015年10月16日genus 種数⇔数⇔ 示性数＝[(点の数)-(線の数)+(面の数)] --- topology(オイラー標数[≒示性数？？？]（Euler characteristic）とは、位相空間のもつある種の構造を特徴付ける「位相不変量」のひとつ →→→四色定理？ i.e. 位相幾何学、複体、ホモロジー、不変量、曲面), 2016年01月30日Galois theory --- cyclic group --巡回群 [11]-b, 2016年03月01日platonic solid正多面体(Euler's observationオイラー標数(局面的多様体において？、位相空間のもつある種の構造を特徴付ける位相不変量のひとつ/・/・/ ・・多様体、基本群、ホモトピー、ホモロジー、コホモロジー、ファイバー束などの、位相空間の不変量として代数系を対応させ、位相的性質を代数的性質に移して研究する・・・・・あくまで、立体を平面的に改造した形が多く？！コンピューターグラフィックスにおいても図形を回転？させると立体的にみえるが・・静止した時点では・・ディスプレイ上では平面的に扱われており・・視覚効果の仕掛け？？として"位相空間の不変量として代数系を対応させ" "位相的性質を代数的性質に移す？"・・・具体的には、座標交換系のようなものとともに（何重にも拡がったもの？！）・・線型代数[行列式]にして表現していくーーー「曲面論」？？？(立体の行列? を平面の行列??にみると・歪んだ行列にみえる??？・これを・なんとか・つじつまを・あわせていくように・していく ?????,)？？)), 2016年04月05日properties --- matrix similarity「相似な行列」(Jordan formジョルダン標準形（正標数の代数閉体上での有限巡回群の表現論はジョルダン標準形の理論で完全に説明がつけられる？（代数的閉体（例えば複素数体）上の正方行列に対する標準形のことである. 任意の正方行列は本質的にただ一つのジョルダン標準形と相似である）), 2017年01月14日Arnold conjectureアーノルド予想 （シンプレクティック同相写像-wiki より）(「オイラー標数<位相空間(オイラー多面体【オイラーの多面体定理】?・・・例えば，クラインの瓶の種数は2である. 多面体の頂点，辺，面の個数をa_0,a_1,a_2とするとき，a_0－a_1＋a_2をオイラー標数という. この数は，多面体が種数nの向きがつけられる閉曲面のときはつねに2－2nとなり，種数nの向きがつけられない閉曲面のときはつねに2－nとなる・/・/・…とくに，多面体の面を含む平面がこの面以外では多面体と交わらないようなものを凸多面体という.
一つの多面体において，その頂点の個数をα0，辺の個数をα_1，面の個数をα2とするとき，α_0－α_1＋α_2をその多面体のオイラー標数(種数)という. 凸多面体ではオイラー標数はつねに2になる・・・・・ )のもつある種の構造を特徴付ける位相不変量のひとつ>」), 2017年05月21日ミンコフスキー空間・ローレンツ変換 etc .. → Influence on later work---/wiki/エルラン ゲン・プログラム(;affine geometry放射幾何学？？ ), 2017年07月07日definition---adjoint representation随伴表現(反交換関係は、体の標数が 2 ではないとき、交代性があることを意味する ), 2017年11月29日Dijkstra's algorithmダイクストラ法（最短経路問題）[4], 2018年02月16日Lagrangian[Theory]---quantum chromodynamics(量子色力学)[22](g を標数0の体上の有限次元リー代数とする ) etc?? ] different from 2, each diagonal element of a skew-symmetric matrix[2017年07月13日skew-symmetric and alternating forms---skew-symmetric (or antisymmetric or antimetric) matrix歪対称行列(反対称行列、交代行列[,alternative matrix ])(対称なテンソル との縮約は恒等的に 0 に等しい(, たいしょうてきなのは？・「0」しかない？.？,？, 双対?でないものを？・・なんとかつじつまあわせて双対にしようとこころみる('computer'じょうでつじつまがあえば・それでいい?? )？！？！,？)) ] must be zero, since each is its own negative.
In linear algebra, a real symmetric matrix represents a self-adjoint operator over a real inner product space実?-計量ベクトル空間上のエルミート作用素[自己共役作用素 ]. The corresponding object for a complex inner product space is a Hermitian matrix「エルミート行列([=self-adjoint matrix自己随伴行列 ] 複素数に成分をとる正方行列で自身の随伴行列（共軛転置）と一致するようなものを言う. エルミート行列は、実対称行列の複素数に対する拡張版の概念として理解することができる. よく知られたパウリ行列、ゲルマン行列および一般化されたそれらはエルミートである. 理論物理学においてそれらのエルミート行列には、しばしば虚数の係数が掛かって「歪エルミート行列([反エルミート行列 ] ~ 自身のエルミート共役が自身に負号をつけたものに等しいような複素正方行列のことである. つまり、n 次正方行列 A に対し、そのエルミート共役を A^* で表すとき、A が歪エルミートならば、以下の条件を満たす.
A ^∗ = − A .
行列 A の成分をあらわに書けば、これは次のようにも表せる.
( A ^∗ ) _{i j} = A _{j i} <hat> ¯ = − A _{i j} ( 1 ≤ i , j ≤ n ) .
歪エルミート行列と似た定義を持つ行列として、エルミート行列がある. エルミート行列は自身と自身のエルミート共役が等しい.
H ^∗ = H .
歪エルミート行列はエルミート行列と同じく、正規行列の特別な場合であり、−1 をユニタリ行列 U と見なせば、以下の正規行列の定義を満たしている.
A ^∗ = A U . 例として、次の行列は歪エルミート行列である.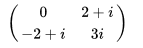 
<figure--歪エルミート行列 > ) 」となる. ) 」 with complex-valued entries, which is equal to its conjugate transpose随伴行列??. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric matrix refers to one which has real-valued entries. Symmetric matrices appear naturally in a variety of applications, and typical numerical linear algebra software makes special accommodations融通(適応?)?調整??? for them. > exactly due to symmetry of the bilinear form. If the n×1 matrix x represents a vector v with respect to this basis, and analogously, y represents w, then B ( v , w ) is given by :
x ^{T} A y = y ^{T} A x .
Suppose C' is another basis for V, with : [ e′_1 ′ ・・・ e′_n ] = [ e _1 ・・・ e _n ] S with S an invertible n×n matrix. Now the new matrix representation for the symmetric bilinear form is given by
A ′ = S ^{T} A S .
by Wikipedia
(立体の行列? を平面の行列??にみると・歪んだ行列にみえる??？・これを・なんとか・つじつまを・あわせていくように・していく ??・ようなもの???・・ accommodations融通(適応[合]?)?調整??? )
<関連, >
エルミート行列
2016年03月31日properties of the determinant--- determinant[1] 行列式
adjugate matrix随伴行列[エルミート随伴(転置) <<(i,j)-余因子を (i,j)-成分に持つ行列を「余因子行列」、その転置行列を随伴行列[エルミート随伴(転置)という？？>>] adj(A)・・・ is the transpose of the matrix consisting of the cofactors, i.e.,
(adj(A))_i,j = (-1)^i+j・[Matrix]_j,i .
2016年04月01日proof---Cramer's rule クラメルの公式[法則]
（列がずれ(反転？[置換？]・・ることによる「基本属性？！」を含蓄する？？・・・{二つの列が同一だと・・けっかが「１」？になってしまう e.x. 1/1=1} ようするに、１のべきじょう根「１の冪根」をけいさんするには、この奇妙な？！？ほうほうしかないのだ！！！---列を[置換？]した勘違いをする、誤認する？？けいさん？？？？？ ）・・・根が一意に決まるような線型方程式系の公式が行列式を用いて表示される？！？（クラメルの公式[法則]）
2016年04月24日series representation---bring radical(ultraradical )超冪根[2]
2016年08月14日linear ooperators---bra–ket notationブラ-ケット記法
2016年08月31日table of interatomic matrix elements原子間行列要素一覧---Tight_binding強結合近似
量子力学では、物理量（観測可能量、オブザーバブル） A は状態ベクトル（もしくは波動関数）にはたらくエルミート演算子 A<hat^> として記述される. 状態 |ψ1> における物理量Aの測定値の平均値は <ψ1|A<hat^>|ψ1> となる. 同様に状態 |ψ2> における物理量Aの測定値の平均値は <ψ2|A<hat^>|ψ2> となる. 量子力学では、重ね合わせて作られた状態 |ψ′> における物理量Aの測定値の平均値 <ψ′|A <hat^>|ψ′> は、<ψ1|A<hat^>|ψ1> と <ψ2|A<hat^>|ψ2> の線形結合では表せない. これを「干渉効果」(きょだいなエネルギーがひそむきけんせい？・・・・・・・)と呼ぶ. <ψ′|A<hat^>|ψ′> ≠ |c_1|^2 <ψ_1|A<hat^>|ψ_1> + |c_2|^2 <ψ_2|A<hat^>|ψ_2>実際には、「干渉項」と呼ばれる余分な項がついてくる. （次の後半の2項）
<ψ′|A<hat^>|ψ′> = |c_1|^2 <ψ_1|A<hat^>|ψ_1> + |c_2|^2 <ψ_2|A<hat^>|ψ_2> + c_1^∗ c_2 <ψ_1|A<hat^>|ψ_2> + c_2^∗ c_1 <ψ2|A<hat^>|ψ1>
2016年09月01日cluster operator---Coupled cluster (CC) 結合クラスター法（ハートリーフォック法の概要？）
"creation and annihilation operators"生成消滅演算子（量子的な調和振動子や多体問題など、量子論において基本変数として広く使われる演算子である.
量子論では、正準変数で量子化することでできた量子論を、生成消滅演算子を基本変数にした量子論に書き換えることがしばしば行われる.
消滅演算子は、状態の粒子の数を1だけ減らす演算子である. 生成演算子は、状態の粒子の数を1だけ増やす演算子で、消滅演算子のエルミート共役をとったものである.
生成消滅演算子は様々な粒子の状態に作用することができる. 例えば、量子化学や多体理論において、生成消滅演算子は電子状態に作用される.
ボース粒子における生成消滅演算子の扱いは、量子的な調和振動子における扱いと同様である. 例えば、同じボース粒子状態に関連する生成消滅演算子の交換子は1に等しく、他のすべての交換子は0である. 一方、フェルミ粒子では状況が異なり、交換子のかわりに反交換子が含まれている）⇔・⇔交換関係 (量子力学)<演算子としてあらわされた物理量が満たす量子力学特有の関係>？！？・・・・・
2016年09月02日Roothaan equations---ハートリー-フォック-ローターン方程式(ローターン方程式)
eigenvalue problem固有値問題[2015年09月10日同ブログ 固有値（問題）→エルミート作用素→ハミルトニアン20150810(不確定性原理)→時間依存しない シュレーディンガー方程式（→時間依存するシュレーディンガー方程式）] because they are nonlinear非線形？:
2017年03月20日Ricci-flat manifoldsリッチ平坦多様体
k -次元の四元数エルミート空間の「四元数線型ユニタリ自己準同型の群(=’holonomy groups’’)」と同一視される
2017年08月10日definition---nuclear space核型空間
2017年08月13日statement of the inequality---Cauchy-Schwarz inequality[Cauchy-Bunyakovsky-Schwarz inequality]コーシー＝シュワルツの不等式
コーシー＝シュワルツの不等式→計量ベクトル空間<, /wiki/Inner_product_space#Examples >(内積と呼ばれる付加的な構造を備えたベクトル空間であり、内積空間（: inner product space）・・・内積はそれに付随するノルムを自然に導き、内積空間はノルム空間の構造を持つ. 内積に付随するノルムの定める距離に関して完備となる空間はヒルベルト空間と呼ばれ、必ずしも完備でない内積空間は（内積の導くノルムに関する完備化がヒルベルト空間となるから）前ヒルベルト空間 (pre-Hilbert space) と呼ばれる. 複素数体上の内積空間はしばしばユニタリ空間 (unitary spaces) とも呼ばれる・・ ・・・)→フビニ・スタディ計量（、射影ヒルベルト空間上のケーラー計量である. つまり、「複素射影空間」 CP^n がエルミート形式を持つことを言う）
2017年08月31日properties---Schatten norm[Schatten-von-Neumann norm]シャッテンノルム
(コーシー＝シュワルツの不等式→計量ベクトル空間<, /wiki/Inner_product_space#Examples >(内積と呼ばれる付加的な構造を備えたベクトル空間であり、内積空間（: inner product space）・・・内積はそれに付随するノルムを自然に導き、内積空間はノルム空間の構造を持つ. 内積に付随するノルムの定める距離に関して完備となる空間はヒルベルト空間と呼ばれ、必ずしも完備でない内積空間は（内積の導くノルムに関する完備化がヒルベルト空間となるから）前ヒルベルト空間 (pre-Hilbert space) と呼ばれる. 複素数体上の内積空間はしばしばユニタリ空間 (unitary spaces) とも呼ばれる・・ ・・・)→フビニ・スタディ計量（、射影ヒルベルト空間上のケーラー計量である. つまり、「複素射影空間」 CP^n がエルミート形式を持つことを言う）))
2017年09月16日example---Riesz–Fischer theoremリース＝フィッシャーの定理（← L^p spaces[1]-- -/wiki/L^p_space )
inner product space内積(空間)（（実または複素）ベクトル空間上で定義される非退化かつ正定値のエルミート半双線型形式（実係数の場合には対称双線型形式）のことである. 二つのベクトルに対してある数（スカラー）を定める演算であるためスカラー積（: scalar product）ともいう. 内積を備えるベクトル空間は内積空間と呼ばれ、内積の定める計量を持つ幾何学的な空間と見做される. エルミート半双線型形式の意味での内積はしばしば、エルミート内積またはユニタリ内積と呼ばれる）
etc.. ??...
ゲルマン行列
2016年07月29日history---quantum chromodynamics(量子色力学)[5]
2016年10月28日history---quantum chromodynamics(量子色力学)[10]
James Bjorken（ジェームズ・ビョルケン("the quark'については、1969年、マレー・ゲルマンが「素粒子の分類と相互作用に関する発見と研究」においてノーベル物理学賞を受賞した・・しかし、彼のこのアイディアはそれにもまさるものとかんがえてもまちがいない<クォークのなかの構成要素としての素粒子？>？！・・・ )
2016年11月18日some definitions[Theory](1)---quantum chromodynamics(量子色力学)[13]
2016年11月19日interpretation of the Lagrange multipliers---method of Lagrange multiplierラグランジュの未定乗数法(→最適化問題[極値?])（ゲルマン行列では？・・λ_k は、１～234567～８まで？！？・/・/・古典にしないと量子では代数化できない？！？！？ ）
2017年01月11日comparison with Riemannian geometry---symplectic<屈折曲面的？> geometryシンプレクティック 幾何学
概複素構造<複素解析的多様体は必ず概複素構造をもつ一方で、"概複素構造'を持ちながら複素解析的多様体とならないものが存在する. 概複素多様体はシンプレクティック幾何学に重要な応用を持つ>Jにも依存した鎖複体を構成？・・ )
2017年07月27日q-hypergeometric functionハイネの和公式('computer'のさんしゅつしたもの,？？)
('computer'のさんしゅつしたもの(他にも？類似物が.多数そんざいする？！・, )に・・人間のせつめいは、むずかしい？？,？ )
etc??...
パウリ行列
2016年08月11日history---quantum chromodynamics(量子色力学)[6] Sir Wolfgang Ernst Pauli
2016年08月14日linear ooperators---bra–ket notationブラ-ケット記法
unitary(U*U = UU* = I、I は単位行列、U* は行列 U の随伴行列 Pauli matricesパウリ行列20160809 etc...)
2016年08月23日total angular momentum quantum number(全角運動量量子数)
azimuthal方位角 quantum number＜《物理》方位量子数、副量子数、軌道量子数◆原子の核外電子の状態を決める4つの量子数の一つ. 4つの量子数quantum numberは（主量子数main-、方位量子数azimuthal-、磁気量子数magnetic-、スピン量子数spin-）. パウリPauliの排他原理によりすべての核外電子はこれらの量子数で定義される（一つの状態には1個の電子しか存在しない）. 方位量子数の記号は「l」. 殻の方位量子数「l」の取り得る値は、n-1、n-2、1、0（nは主量子数main quantum number）. 方位量子数「l」は、0＝s、1＝p、2＝d、3＝f、4＝g、5＝h、6＝i、7＝k、で表す（s, p,d, fは分光学のsharp、principal、diffuse、fundamental から）. 方位量子数で細分化された殻を亜殻subshellと呼ぶ・・・あくまで微分、積分、行列等をつかって線型であらわそうとしている？(computer のために)・・各元素固有の性質が決定されるために？！・・・電子がどのような軌道に配置しているのか近似的に表す(「一体近似で得られる原子軌道あるいは分子軌道に複数の電子が詰まった状態」)？？・・・＞
2017年09月22日Dual spaces(Properties of L^p spaces[5])---/wiki/L^p_space
電子は、ひとつひとつ別々なそんざい(パウリの定理パウリの排他律、パウリの禁制)ーーPauli matricesパウリ行列のたんじょう・・？？・・・このはっけんにより、「そりゅうしぶつりがく」はいちじるしいはってんをむかえる（高エネルギー物理学）？！？・・)
2018年02月22日general behavior---/wiki/system of linear equations行列の基本変形(解法)？ーー/wiki/線型方程式系
パウリPauliの排他原理によりすべての核外電子はこれらの量子数で定義される（一つの状態には1個の電子しか存在しない）. 方位量子数の記号は「l」. 殻の方位量子数「l」の取り得る値は、n-1、n-2、1、0（nは主量子数main quantum number）. 方位量子数「l」は、0＝s、1＝p、2＝d、3＝f、4＝g、5＝h、6＝i、7＝k、で表す（s, p,d, fは分光学のsharp、principal、diffuse、fundamental から）. 方位量子数で細分化された殻を亜殻subshellと呼ぶ・・・あくまで微分、積分、行列等をつかって線型であらわそうとしている？(computer のために)・・各元素固有の性質が決定されるために？！・・・電子がどのような軌道に配置しているのか近似的に表す(「一体近似で得られる原子軌道あるいは分子軌道に複数の電子が詰まった状態」)？？・・・
etc .....
Robertgal@
