
|
|
|
テーマ:建築業界応援!(1038)
カテゴリ:建築士受験!!
構造力学編第4回(トラス) 建築士試験に独学で挑戦する方のために、過去問を使って問題の解き方・ポイント・解説などを行っています。 過去問約20年分を1肢ごとにばらして、出題の項目ごとに分けてまとめています。1,2級両方載せていますので、1級受験の方は2級問題で慣らしてから1級問題に挑戦。2級受験の方は、時々1級の過去問題からも出題されますので参考程度に1級問題を見ておくと得点UPが狙えます!! 全科目終わるには先の長い話ですが、勉強の参考になると嬉しいです! 構造-8 構造の問題は大きく構造力学(計算問題)と各種構造・建築材料(文章問題)に分かれます。ここでは、計算問題と文章問題を交互に紹介していきます。 構造(力学) 4.トラス 今回は、力学のトラスです。苦手な方が多い問題ですが、トラスと言っても今までやってきた応力の問題と同じなんです! トラスは軸力しかかからないので、曲げやせん断は考える必要がなく、軸力のみ求めればいいんです。ただ、引張(+)なのか圧縮(-)なのかで迷う人が多いですね。原則、引張(+)方向に仮定して、答えが-と出てきたら圧縮(-)と判断すればいいんです。あと、①0部材、②十字部材、③三角形の先端、この三つの考え方は覚えておくと簡単に解ける問題もあります!!(詳しくは解説で) (問題は、一部修正しているものもあります。) *************************************************************** 問題 □ トラス 1-1 トラス(2級) 1 図のような荷重を受ける静定トラスにおいて、斜材Aに生じる軸力として、正しいもの は、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とする。 (2級H14) 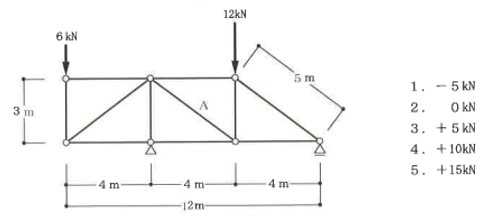 2 図のような荷重を受ける静定トラスにおいて、部材Aに生じる軸方向力として、正しいも のは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とする。 (2級H15)  3 図のような荷重を受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力の組み 合わせとして、正しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」 、圧縮力を「-」とする。(2級H16) 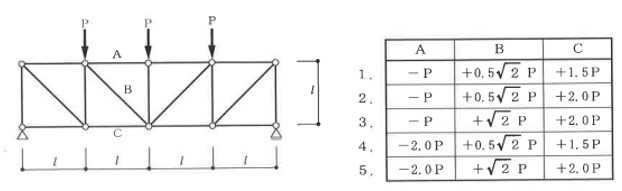 4 図のような外力を受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力の組み 合わせとして、正しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」 、圧縮力を「-」とする。(2級H17) 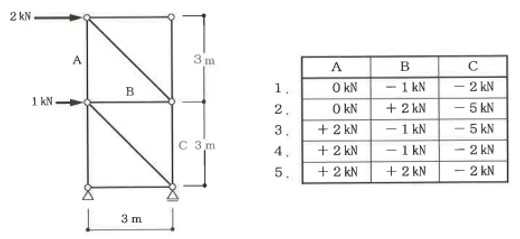 5 図のような荷重を受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力の組み 合わせとして、正しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」 、圧縮力を「-」とする。(2級H18) 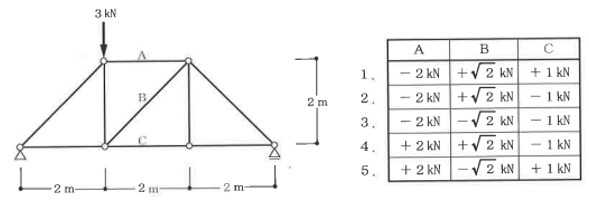 6 図のような荷重を受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力の組み 合わせとして、正しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」 、圧縮力を「-」とする。(2級H19)  7 図のような荷重を受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力NA、NB、 NCの組み合わせとして、正しいものは、次のうちどれか。ただし、軸方向力は、引張力 を「+」、圧縮力を「-」とする。(2級H20) 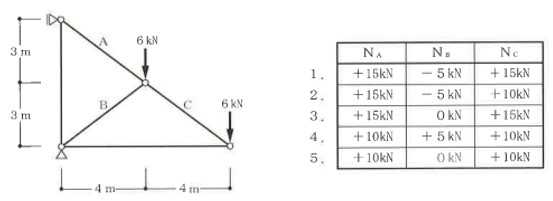 8 図のような下向きの荷重Pを受ける静定トラスにおいて、部材A、B、Cに生じる圧縮力・ 引張力の組み合わせとして、正しいものは、次のうちどれか。(2級H21) 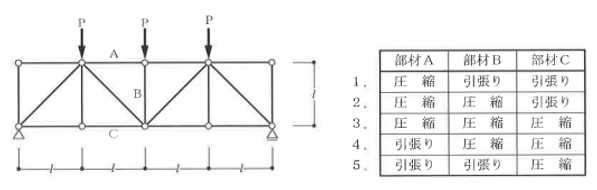 9 図のような外力を受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力の組み合 わせとして、正しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、 圧縮力を「-」とする。(2級H22)  10 図のような荷重を受ける静定トラスにおいて、部材Aに生じる軸方向力として、正しい ものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とす る。(2級H23) 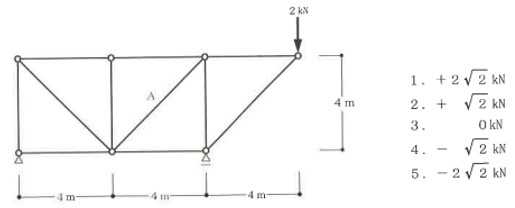 11 図のような荷重を受ける静定トラスにおいて、部材Aに生じる軸方向力として、正しい ものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とす る。なお、接転間距離はすべて2mとする。(2級H24) 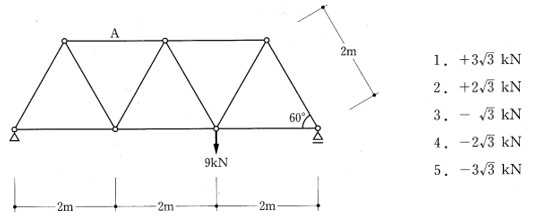 12 図のような荷重を受ける静定トラスにおいて、部材Aに生じる軸方向力として、正しい ものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とす る。なお、接転間距離はすべて2mとする。(2級H25) 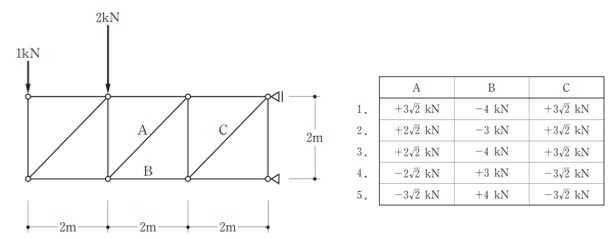 13 図のような外力を受ける静定トラスにおいて、部材Aに生じる軸方向力として、正しい ものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とす る。(2級H26)  14 図のような荷重P受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力の組み合 わせとして、正しいものは、次のうちどれか。(2級H27) 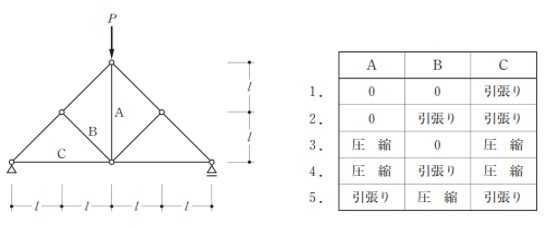 15 図のような外力を受ける静定トラスにおいて、部材Aに生じる軸方向力の値として、正 しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」 とする。(2級H28) 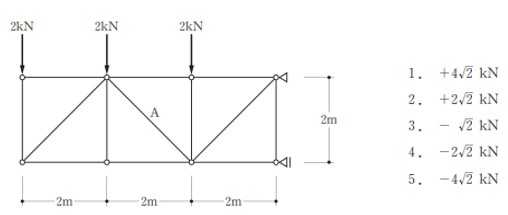 16 図のような外力を受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力の組み合 わせとして、正しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、 圧縮力を「-」とする。(2級H29) 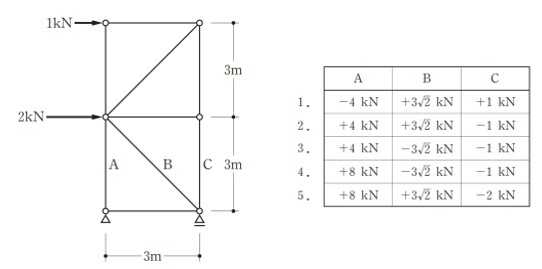 17 図のような外力を受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力の組み合 わせとして、正しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、 圧縮力を「-」とする。(2級H30) 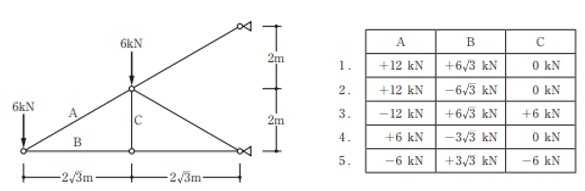 18 図のような荷重P受ける静定トラスにおいて、部材A、B、Cに生じる軸方向力の組み合 わせとして、正しいものは、次のうちどれか。(2級R01) 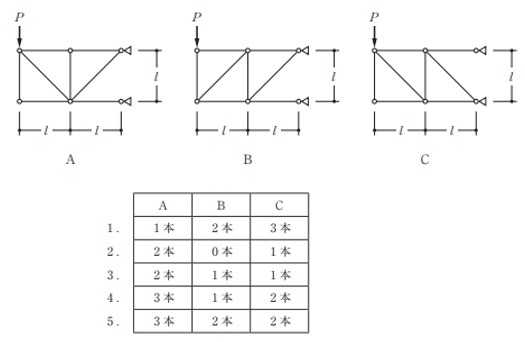 19 図のような外力を受ける静定トラスにおいて、部材Aに生じる軸方向力の値として、正 しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」 とする。(2級R02)  20 図のような荷重条件が異なる静定トラスA、B、Cにおいて、軸方向力が生じない部材の 本数の組み合わせとして、正しいものは、次のうちどれか。ただし、荷重条件以外の条 件は、同一であるものとする。(2級R03) 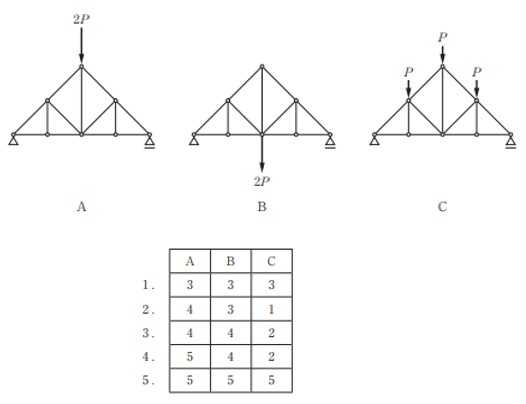 21 図のような外力を受ける静定トラスにおいて、支点Bに生じる鉛直反力VBと部材AB、 CDにそれぞれ生じる軸方向力NAB、NCDの組み合わせとして、正しいものは、次のう ちどれか。ただし、鉛直反力の方向は上向きを[+]、下向きを[-]とし、軸方向力は、 引張力を「+」、圧縮力を「-」とする。(2級R04)  1-2 トラス(1級) 1 図のような荷重を受けるトラスにおいて、上弦材ABに生じる軸方向力として、正しい ものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とす る。(1級H17) 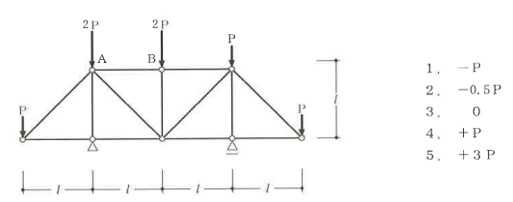 2 図のような荷重を受けるトラスにおいて、部材ABに生じる軸方向力として、正しいも のは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とす る。(1級H18) 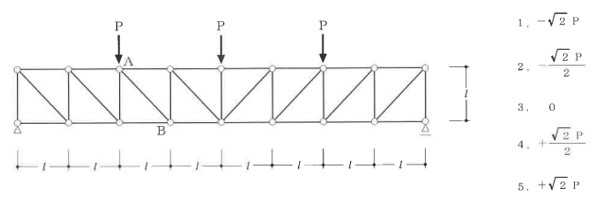 3 図のような荷重を受けるトラスにおいて、部材ABに生じる軸方向力として、正しいも のは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とす る。(1級H19)  4 図のような荷重を受けるトラスにおいて、部材ABに生じる軸方向力として、正しいも のは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とす る。(1級H20) 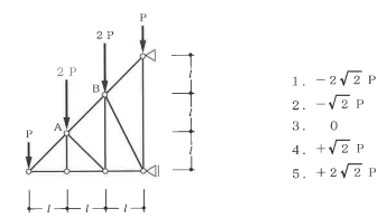 5 図のような荷重Pを受けるトラスにおいて、部材ABに生じる軸方向力として、正しいも のは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とす る。(1級H23) 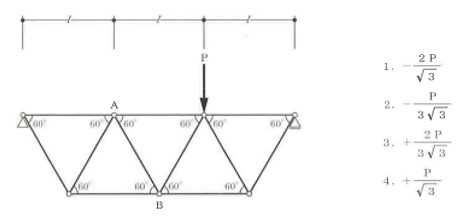 6 図のような荷重が作用するトラスにおいて、部材ABに生じる軸方向力として、正しいも のは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とする。 (1級H24) 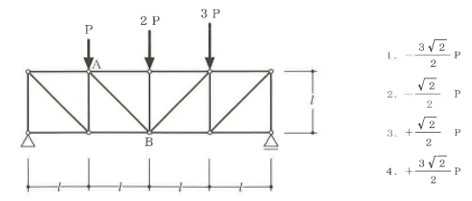 7 図のようなトラスに荷重Pが作用したときの部材ABに生じる軸方向力として、正しいも のは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とする。 (1級H25) 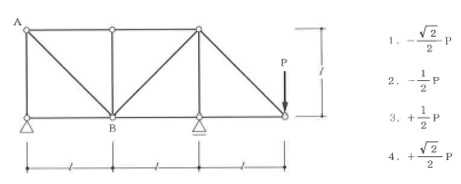 8 図のような水平荷重が作用するトラスにおいて、部材A~Eに生じる軸力の組合わせとし て、正しいものは、次のうちどれか。ただし、表中「引」は引張力、「圧」は圧縮力を 示す。(1級H26)  9 図のような鉛直荷重Pを受けるトラスにおいて、部材ABに生じる軸方向力として、正し いものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」と する。(1級H27) 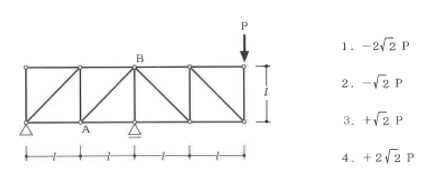 10 図のような鉛直荷重が作用するトラスにおいて、部材ABに生じる軸方向力として、正し いものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」と する。(1級H28)  11 図のような荷重が作用するトラスにおいて、部材ABに生じる軸方向力として、正しいも のは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とする。 (1級H29)  12 図のような水平荷重Pが作用するトラスにおいて、部材A及びBに生じる軸力の組合わせ として、正しいものは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮 力を「-」とする。(1級H30) 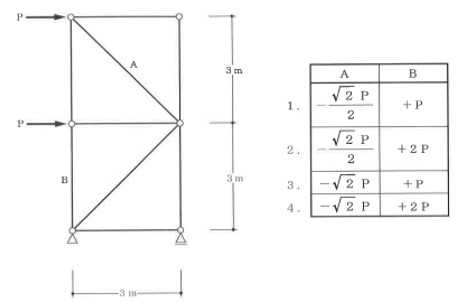 13 図のような荷重が作用するトラスにおいて、部材ABに生じる軸方向力として、正しいも のは、次のうちどれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とする。 (1級R01) 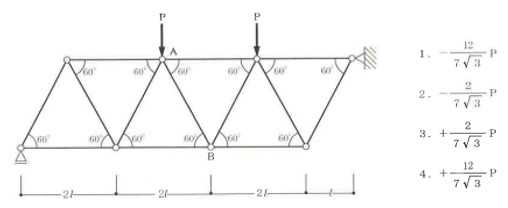 14 図のような荷重が作用するトラスにおいて、部材A、B、C及びDに生じる軸方向力をそれ ぞれNA、NB、NC及びNDとするとき、それらの値として、誤っているものは、次のうち どれか。ただし、軸方向力は、引張力を「+」、圧縮力を「-」とする。(1級R02) 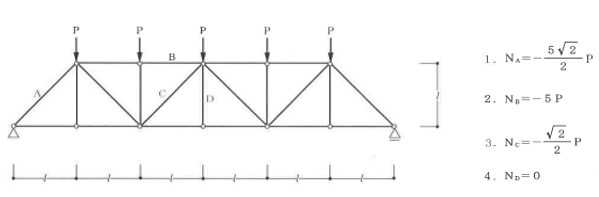 15 図のような荷重が作用するトラスにおいて、部材A、B及びCに生じる軸方向力をそれ ぞれNA、NB及びNCとするとき、それらの大小関係として、正しいものは、次のうちど れか。ただし、 全ての部材は弾性部材とし、自重は無視する。また、軸方向力は、引張 力を「+」、圧縮力を「-」とす る。(1級R04) 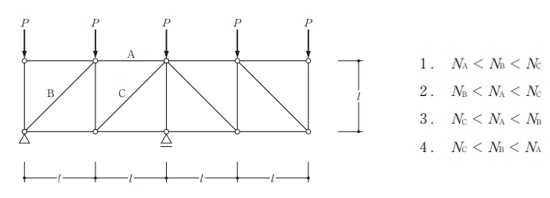 ***************************************************************** 解説 □ トラスの解き方 ① 0部材を見極める! ・2コか3コの法則!(接点に対して、角度をもった2つの部材は2つとも軸力は0となる。 接点に対して、3つの部材のうち2つは直線の場合残りの1部材は軸力0となる)  ② 十字部材を見極める! ・接点に対して十字に部材がある場合、ΣX=0、ΣY=0が成り立つ 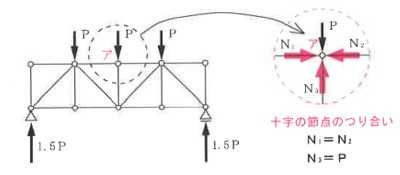 ③ 三角形の先端を見極める! ・接点に対して角度をもって三つの部材があるとき、一つの力が解れば三角比で求めることが できる。その際、接点を襲ている部材は「圧縮」、接点を引張っている部材は「引張」と判 断する。 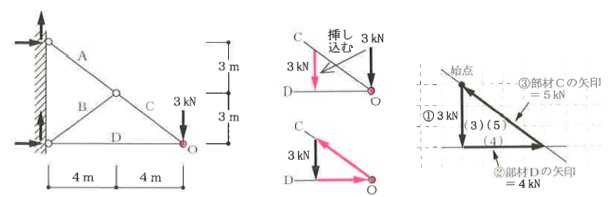 ④ 切断法(一般的な応力の求め方と同じ) 1) 反力を仮定して、図中に書き入れる。 2) 応力を求める位置で構造物を左右(上下)に切断し、何方か一方を選択する。選択する方に 支点があれば、切断する前に反力を求める。 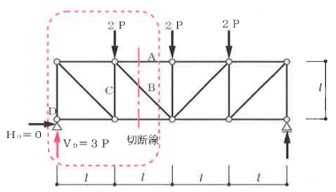 3) 切断した図を描き、切断位置に応力を仮定し、図の中に書き入れる。(切断位置より外側 に軸力の方向を仮定する。引張側に仮定)  4) つり合い条件式により、応力を求める。 ・NAは、ΣMO=0より求める。 NBは、X,Yに分解してΣY=0より求め、三角比によりる斜め に戻す。NCは、ΣY=0より求める。 5) 応力の向きを検討する。 6) 仮定と同じ方向(切断位置から外側向き)は引張、逆は圧縮と判断する 1-1 トラス(2級) 1 切断法で求める。ΣMB=0より、反力VCを求める。 -6KN×4m+12KN×4m-VC×8m=0 VC=3KN(↑) NAをX,Y成分に分解し、ΣY=0より、NAYを求める。 -12KN+3KN+NAY=0 NAY=9KN(↑) 三角比よりNAを求める。5:NA=3:9KN NA=15KN(引張) 正解 5番 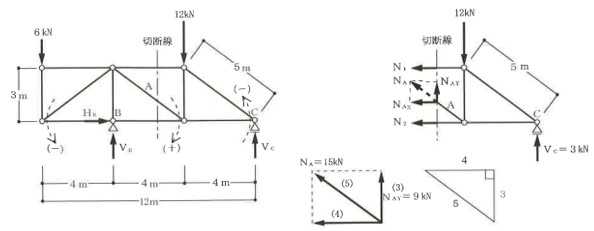 2 切断法で求める。ΣMB=0より、反力VCを求める。 -3KN×4m-VC×4m=0 VC=3KN(↓) ΣY=0より、NAを求める。-2KN-3KN-NA=0 NA=-9KN(圧縮) 正解 1番 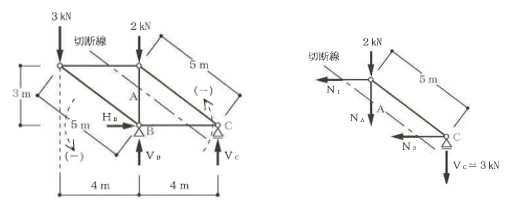 3 切断法で求める。反力VD=1.5P(↑)(式省略) ΣMO=0より、NAを求める。 +1.5P2ℓ-P×ℓ+NA×ℓ=0 NA=-2P(圧縮) NBをX,Y成分に分解し、ΣY=0よりNBYを求める。 +1.5P-P-NBY=0 NBY=0.5P(↓) 三角比よりNBを求める。1:0.5P=√2:NB NB=0.5√2P(引張) ΣMA=0より、NCを求める。+1.5P×ℓ-NC×ℓ=0 NC=1.5P(引張) 正解 4番 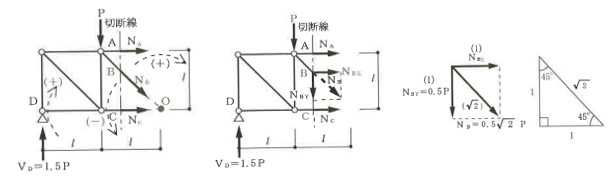 4 切断法で求める。ΣMO=0より、NAを求める。 +2KN×3m-NA×3m=0 NA=2KN(引張) ΣX=0よりNBを求める。+2KN-NB=0 NB=2KN(引張) ΣMQ=0より、NCを求める。+2KN×3m+NC×3m=0 NC=-2KN(圧縮) 正解 5番 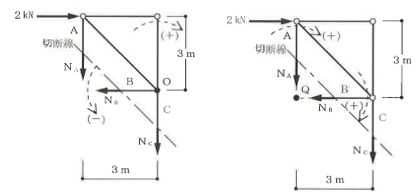 5 切断法で求める。反力VE=1KN(↑)(式省略) ΣMO=0より、NAを求める。 -1KN×4m-NA×2m=0 NA=-2KN(圧縮) NBをX,Y成分に分解し、ΣY=0よりNBYを求める。 +1KN-NBY=0 NBY=1KN(↓) 三角比よりNBを求める。1:1=√2:NB NB=√2P(引張) ΣMQ=0より、NCを求める。-1KN×2m+NC×2m=0 NC=1KN(引張) 正解 1番 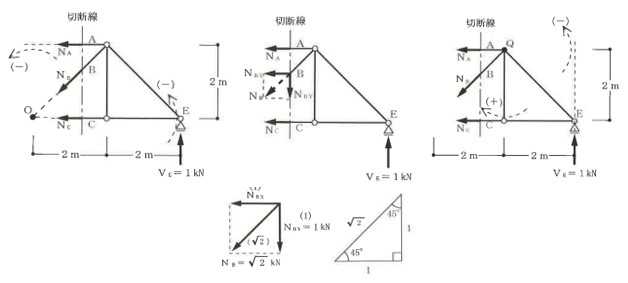 6 NAは十字部材により、NA=-3KN(圧縮) NCは0部材、NC=0 NBは切断法で求める。NBをX,Y成分に分解し、ΣX=0よりNBXを求める。 +4KN-NBX=0 NBX=4KN(←) 三角比よりNBを求める。4:3=5:NB NB=5KN(引張) 正解 2番 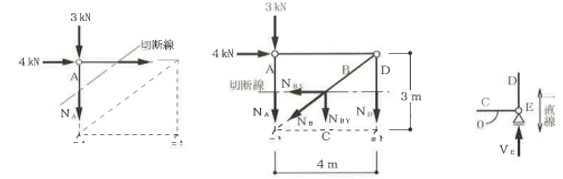 7 NCは三角形の先端より、NC=10KN(引張) NA、NBは切断法で求める。ΣMQ=0より、NAを求める。 +6KN×4m+6KN×8m-NA×4.8m(三角比より距離を求める)=0 NA=15KN(引張) ΣMO=0より、NBを求める。 -6KN×4m-NB×4.8m(三角比より距離を求める)=0 NB=5KN(引張) 正解 2番 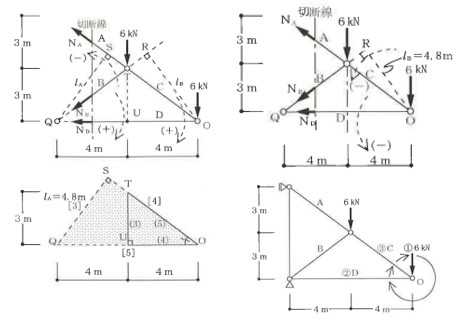 8 NBは十字部材なので、NB=-P(圧縮) NA、NCは切断法で求める。 反力VD=1.5P(↑)(式省略) ΣMO=0より、NAを求める。 +1.5P×2ℓ-P×ℓ+NA×ℓ=0 NA=-2P(圧縮) ΣMQ=0より、NCを求める。+1.5P×ℓ-NC×ℓ=0 NC=1.5P(引張) 正解 2番 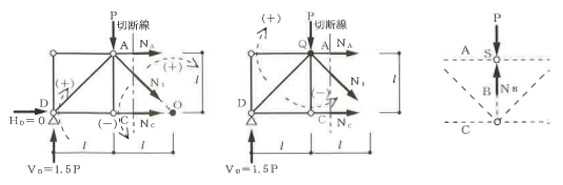 9 切断法で求める。ΣMO=0より、NAを求める。+1KN×3m-NA×3m=0 NA=1KN(引張) ΣMQ=0より、NCを求める。+1KN×3m+NC×3m=0 NC=-1KN(圧縮) ΣX=0より、NBを求める。+1KN-N=0 NB=1KN(引張) 正解 4番 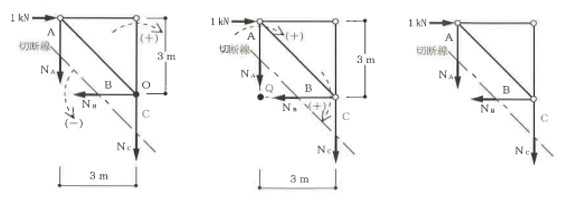 10 切断法で求める。反力VC=3KN(↑)(式省略) NAをX,Y成分に分解して、ΣY=0よりNAYを求める。 -2KN+3KN-NAY=0 NAY=1KN(↓) 三角比よりNAを求める。 1:1=√2:NA NA=√2KN(引張) 正解 2番 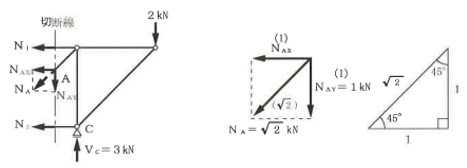 11 切断法で求める。反力VB=3KN(↑)(式省略) ΣMO=0よりNAを求める。 +3KN×2m+NA×√3=0 NA=-6/√3KN 分母側に√があるので有理化する。 -6/√3×√3/√3=-2√3(圧縮) 正解 4番 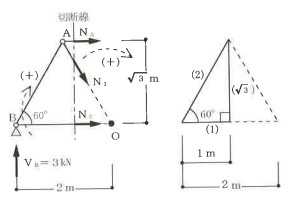 12 切断法で求める。ΣMO=0よりNBを求める。 -1KN×4m-2KN×2m-NB×2m=0 NB=-4KN(圧縮) NAをX,Y成分に分解、ΣY=0よりNAYを求める。 -1KN-2KN+NAY=0 NAY=3KN(↑) 三角比よりNAを求める。1:3=√2:NA NA=3√2KN(引張) NCもNAと同様に求める NC=3√2KN(引張) 正解 1番 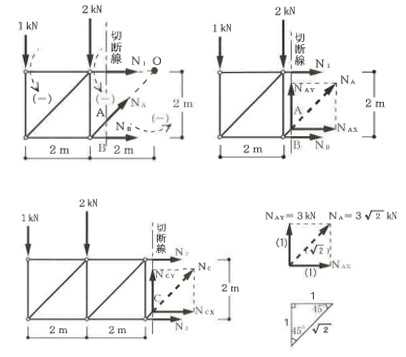 13 切断法で求める。反力VB=2KN(↑)(式省略) NAをX,Y成分に分解、ΣY=0よりNAYを求める。 +2KN+NAY=0 NAY=-2KN(↓) 三角比よりNAを求める。1:-2=√2:NA NA=-2√2KN(圧縮) 正解 5番 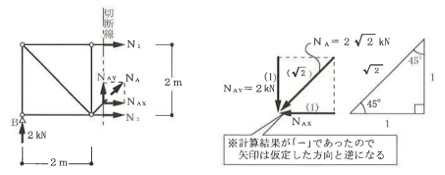 14 NBとNCは0部材より、NB=0、NC=0 反力VEは上向き反力(↑) 三角形の先端より、NC=引張 正解 1番  15 切断法で求める。NAをX,Y成分に分解、ΣY=0よりNAYを求める。 -2KN-2KN-NAY=0 NAY=-4KN(↑) 三角比よりNAを求める。1:-4=√2:NA NA=-4√2KN(圧縮) 正解 5番 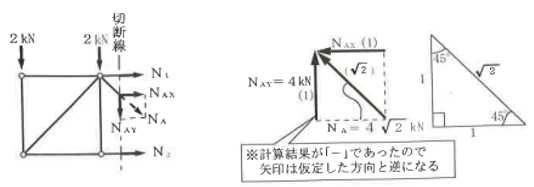 16 切断法で求める。ΣMD=0より、NAを求める。 1KN×6m+2KN×3m-NA×3m=0 NA=4KN(引張) ΣME=0よりNCを求める。1KN×3m+NC×3m=0 NC=-1KN(圧縮) NBをX,Y成分に分解、ΣY=0よりNBXを求める。 1KN+2KN+NBX=0 NBX=-3KN(←) 三角比よりNBを求める。1:-3=√2:NB NB=-3√2KN(圧縮) 正解 3番  17 三角形の先端より、NA=+12KN(引張)、NB=-6√3(圧縮) 0部材より、NC=0 正解 2番 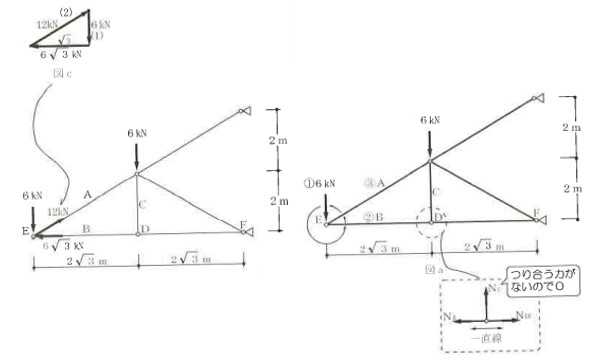 18 0部材より、A=3本、B=1本、C=2本 正解 4番  19 切断法で求める。反力VC=1KN(↑)(式省略) NAをX,Y成分に分解、ΣY=0よりNAYを求める。1KN+NAY=0 NAY=-1KN(↓) 三角比よりNAを求める。1:-1=√2:NA NA=-√2KN(圧縮) 正解 2番 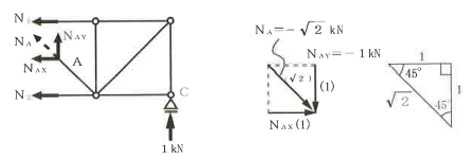 20 0部材より、A=5本、B=4本、C=2本 正解 4番  21 ΣMA=0よりVBを求める。10KN×4m-VB×2m=0 VB=20KN(↑) 切断法によりNABを求める。 ΣMO=0より -20×1m+10KN×2m+NAB×2m=0 NAB=0 NCDは0部材により、NCD=0 正解 1番 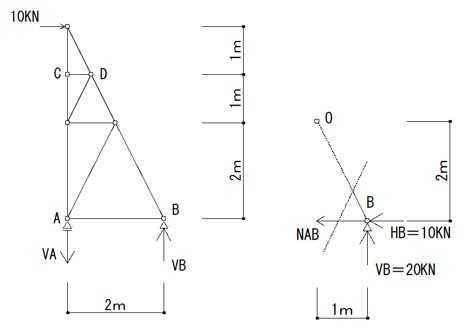 1-2 トラス(1級) 1 切断法で求める。反力VD=4P(式省略) ΣMC=0よりNABを求める。 -P×2ℓ-2P×ℓ+4P×ℓ+NAB×ℓ=0 NAB=20KN(↑) NAB=0 正解 3番 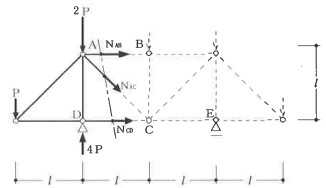 2 切断法で求める。反力VC=1.5P(式省略) NABをX,Y成分に分解、ΣY=0よりNABYを求める。 1.5P-P-NABY=0 NABY=1/2P(↓) 三角比よりNABを求める。1:1/2=√2:NAB NAB=+P√2/2(引張) 正解 4番 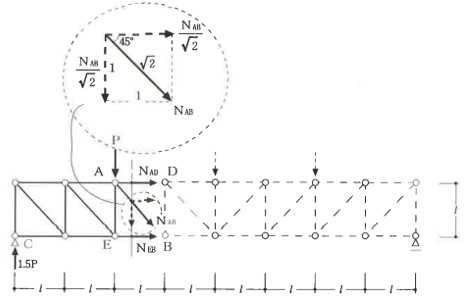 3 NBD、NBEは0部材なので、B点は十字部材となる。NAB=+P(引張) 正解 4番 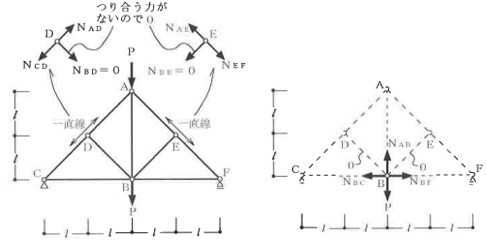 4 切断法で求める。ΣMD=0よりNABを求める。 -P×2ℓ-2P×ℓ+NAB×√2ℓ=0 NAB=+4P/√2 有理化して4P/√2×√2/√2=+2P√2(引張) 正解 5番  5 切断法で求める。左側支点の反力V=1P/3(↑)(式省略) NABをX,Y成分に分解、ΣY=0よりNABYを求める。 +1P/3-NABY=0 NABY=1/3P(↓) 三角比よりNABを求める。√3:1P/3=2:NAB NAB=+2P/3√3(引張) 正解 3番 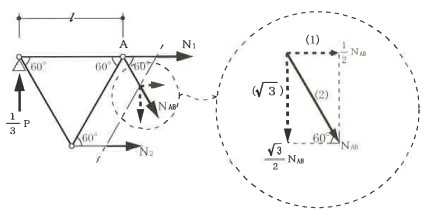 6 切断法で求める。反力VC=5P/2(↑)(式省略) NABをX,Y成分に分解、ΣY=0よりNABYを求める。 +5P/2-P-NABY=0 NABY=3P/2(↓) 三角比よりNABを求める。1:3P/2=√2:NAB NAB=+3P√2/2(引張) 正解 4番 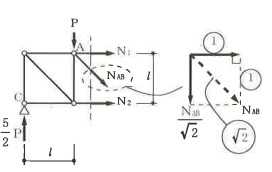 7 切断法で求める。反力VC=P/2(↓)(式省略) NABをX,Y成分に分解、ΣY=0よりNABYを求める。 -P/2-NABY=0 NABY=-P/2(↑) 三角比よりNABを求める。1:-P/2=√2:NAB NAB=-P√2/2(引張) 正番 1番 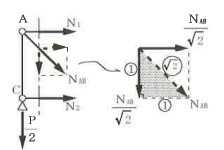 8 F点で三角形の先端を考えると、NC=圧縮、NB=引張 G点で考えると、反力VGは下向きとなるので、三角形の先端からNA=引張、 NE=圧縮 NDは切断法で考えΣMF=0より、荷重Pが反時計回りなのでNDは 時計回りでないと釣り合わないので仮定の向きと逆になる。ND=圧縮 正番 1番 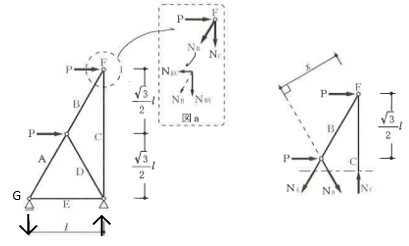 9 切断法で求める。反力VC=P(↓)(式省略) NABをX,Y成分に分解、ΣY=0よりNABYを求める。 -P+NABY=0 NABY=P(↑) 三角比よりNABを求める。1:P=√2:NAB NAB=+P√2(引張) 正解 3番 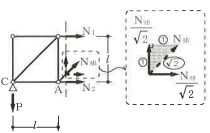 10 切断法で求める。反力VC=2P(↑)(式省略) ΣMO=0よりNABを求める。 2P×3ℓ/2-P×3ℓ/4-NAB×ℓ√3/2=0 NAB=+18P/4√3 有理化して+3P√3/2(引張) 正解 4番 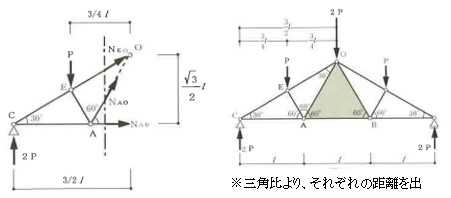 11 切断法で求める。左側支点反力V=2P(↑)(式省略) NABをX,Y成分に分解、ΣY=0よりNABYを求める。 +2P-P-NABY=0 NABY=P(↑) 三角比よりNABを求める。1:P=√2:NAB NAB=+P√2(引張) 正解 4番 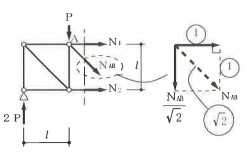 12 切断法で求める。NAをX,Y成分に分解、ΣX=0よりNAXを求める。 +P+NAX=0 NAX=-P(←) 三角比よりNAを求める。1:P=√2:NA NAB=-P√2(圧縮) ΣMC=0よりNBを求める。P×3m-NB×3m=0 NB=P(引張) 正解 3番 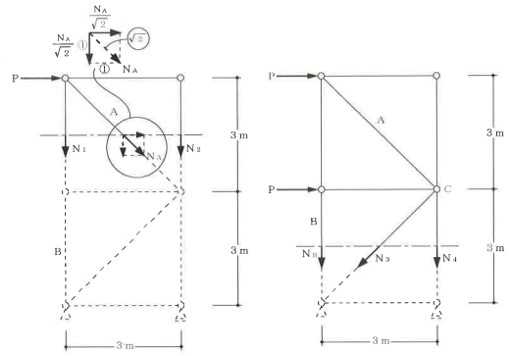 13 切断法で求める。反力VC=6/7P(↑)(式省略) NABをX,Y成分に分解、ΣY=0よりNABYを求める。 +6P/7-P-NABY=0 NABY=-P/7(↑) 三角比よりNABを求める。√3:-P/7P=2:NAB NAB=-2P/7√3(圧縮) 正解 2番 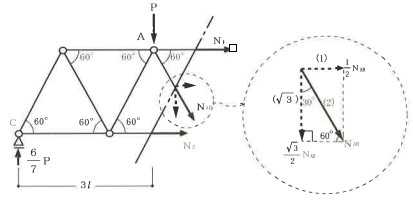 14 反力V=5P/2(↑)(式省略) 三角形の先端よりNAを求める。1:5P/2=√2:NA NA=-5P√2/2(圧縮) 切断法で求める。ΣME=0よりNBを求める。 5P/2×2ℓ-P×ℓ+NB×ℓ=0 NB=-4P(圧縮) NCをX,Y成分に分解、ΣY=0よりNCYを求める。 +5P/2-P-P+NCY=0 NCY=-P/2(↓) 三角比よりNCを求める。1:-P/2=√2:NC NC=-P√2/2(圧縮) 0部材より、ND=0 正解 2番 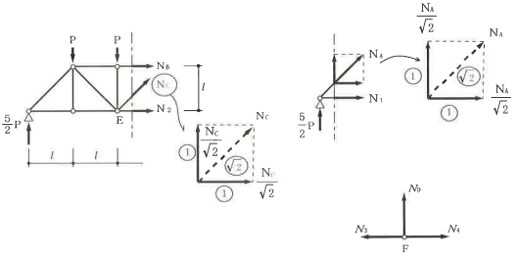 15 切断法で求める。反力VE=0(式省略) NBをX,Y成分に分解、ΣY=0よりNBYを求める。 -P+NBY=0 NBY=P(↑) 三角比よりNBを求める。1:P=√2:NB NB=P√2(引張) ΣMF=0よりNAを求める。-P×ℓ+NA×ℓ=0 NA=P(引張) NCをX,Y成分に分解、ΣY=0よりNCYを求める。 -P-P+NCY=0 NCY=2P(↑) 三角比よりNBを求める。1:2P=√2:NC NC=2P√2(引張)∴NA<NB<NC 正解 1番  今回は力学のトラスの問題でした。力学の中では苦手な方が多い問題の一つですが、三つのポイント①0部材、②十字部材、③三角形の先端は必ず覚えて下さい。切断法はどんな問題でも使えますが、この三つのポイントを使えばもっと簡単に解ける問題が多くあります。次回は文章問題の各種構造へ入っていきます。RC造・S造。木造が中心ですが文章問題では最もよく出題されている分野です!! 今日はこんな言葉です! 『仕事をする時、この仕事が好きだと思わなければ、
仕事のほうがついてきてくれません。 相手が心を打たれるような情熱がなければ、何事 もうまくいくわけがありません。』 (瀬戸内寂聴) お気に入りの記事を「いいね!」で応援しよう
Last updated
Sep 17, 2022 11:49:05 AM
コメント(0) | コメントを書く
[建築士受験!!] カテゴリの最新記事
|
|