
|
|
|
カテゴリ:【数学】
多角形の作図は、分度器を使うと簡単です。
円を描いた後、中心の360°を分度器で分割すれば良いのです。 一周360°を120°で3分割すれば、正3角形になります。 72°なら5角形、60°なら6角形が、コンパスを使わなくても作図できます。 つまり、360が割り切れる数なら作図ができて、 割り切れないと作図ができないのです。 360°は7では割り切れないため、分度器では作図不可能であり、 それはコンパスを使っても作図不可能であることを示しています。 ---------- 正多角形の研究は非常に古く、紀元前300年頃に書かれた、 エウクレイデス(ユークリッド)の著作である 『原論』 にこう記されています。 『正3角形、正方形、正5角形、正15角形や、 それらの2の累乗(2の倍々)の頂点を持つ正多角形は作図可能』 簡単に言うと、 『辺の数で、円角度一回りの360度を割り切れない数(の辺)は作図できない』 というもので、最初の分度器での作図方法と同じことです。  図1 : ユークリッドの名前の方が有名 (互除法の説明が載っていますが、気にしないでください。 ユークリッドの画像が、この画像しかなかったのです) 確かに、綺麗に割り切れない角度を、どうして作図できましょう。 『360°を割り切れない、7、11、13,17、19…(延々続く)の正多角形は作図できない』 その、ぐうの音も出ない完璧な理論は、それ以後2000年間信じられてきました。 ---------- …しかし、その日がやってきました。 実は 『正17角形は作図可能』 であったのです。 それは、1796年3月30日の朝、19歳(!)であったガウスが、 起床した瞬間に気が付いたそうです。 2000年ものあいだ、誰ひとり疑うことがなく信じ続けられた理論を、 起きぬけに吹っ飛ばしたのです。 生まれてすぐに天上天下唯我独尊とおっしゃった釈迦も変態ですが、 このガウスの起きぬけの閃きも、負けず劣らず変態的です。  図2 : ガウス その変態ぶりは、下の青枠で囲った式を暗算で導いたことからわかります。 自分なら確実に、変な式がよぎったと思って二度寝します。 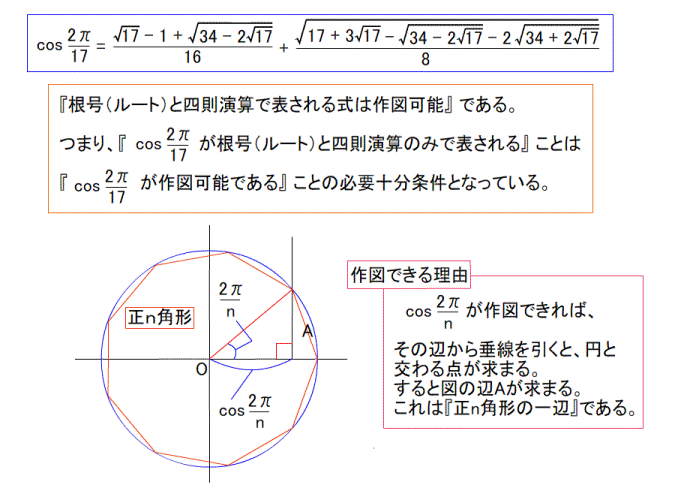 図3 : 正17角形の作図可能を示す式 なんだか小難しいことが書いてありますが、最初に書いてあるように 『ルートと ×÷+- で表現される式はどんなに複雑でも作図可能』 ということなのです。 (『2π』 というのは、角度の360°と同じ意味。 cos●は、図3の下に書いてある三角形の、底辺と同じ。) ガウスが閃いたその式は、暗算で導いたとはとても信じられません。 自分は手計算でも自信がありません。 暗算が異常に得意な数学者は歴史上数多くいますが、ガウスは飛びぬけていました。 そして数学の女神に愛されたが如く、数学センスが抜群でした。 ---------- さて、アンビリーバボーな紀文・・・いや気分のまま、作図方法を解説します。 まあ、ウィキペディアに 『正17角形の作図』 の動画が一応載っているのですが、 あんなもので理解できるのでしょうか。 自分は理解できなかったので、ちまちま作ったのが次の図です。 ぺろんぺろんの、はんぺん気分のままだと確実に混乱するので 気を引き締めてご覧ください。 (作図に文章を書かないのは自分のスタイルなので、わかりにくかったらすいません) 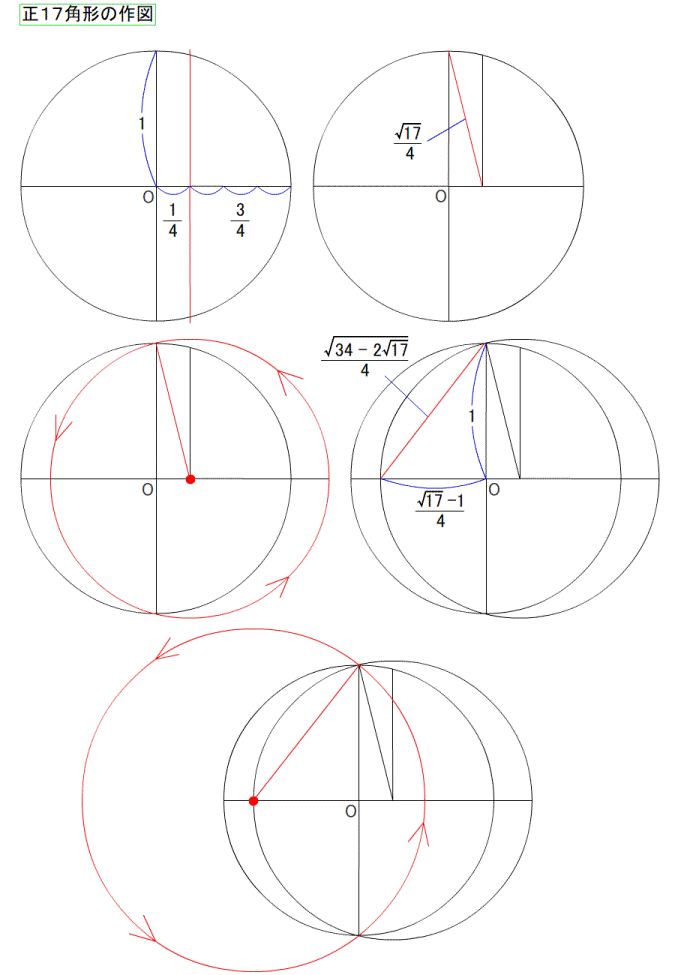 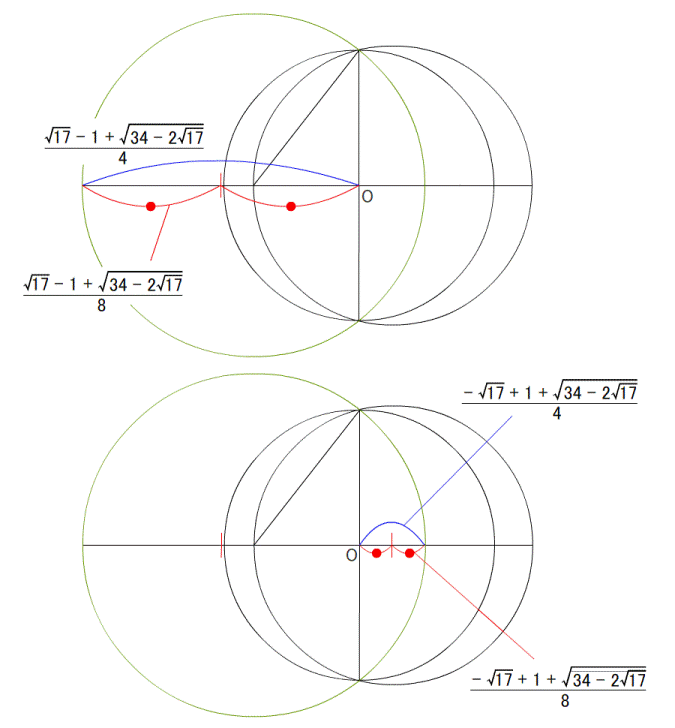 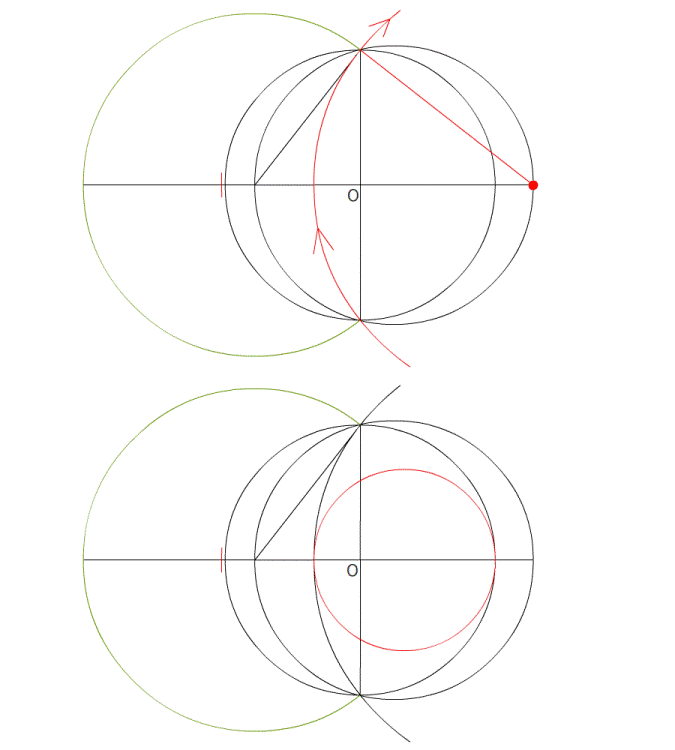 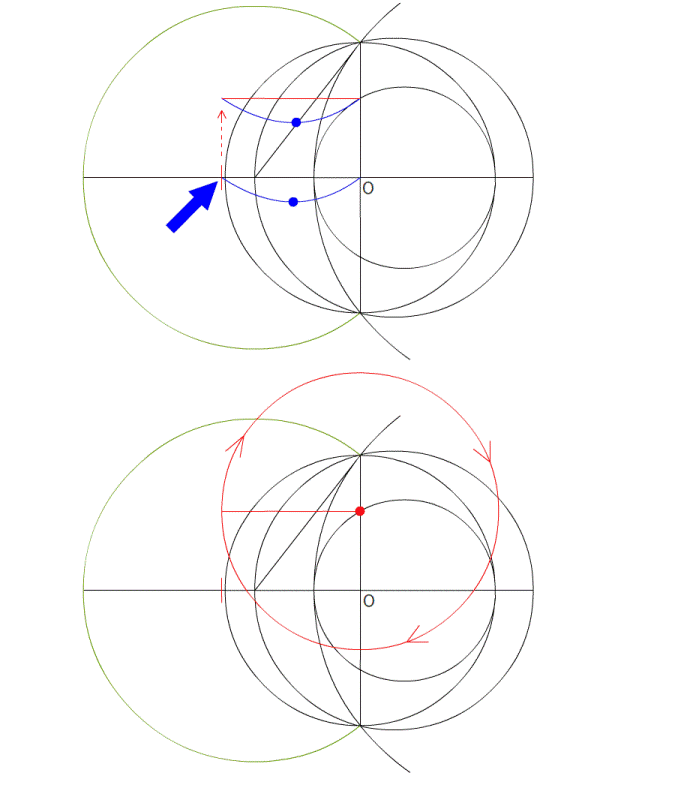 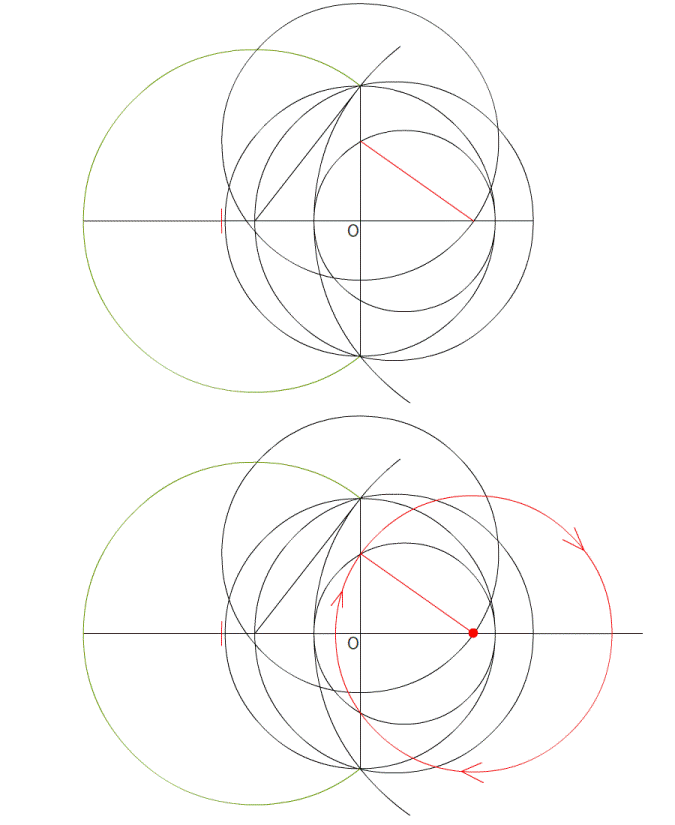 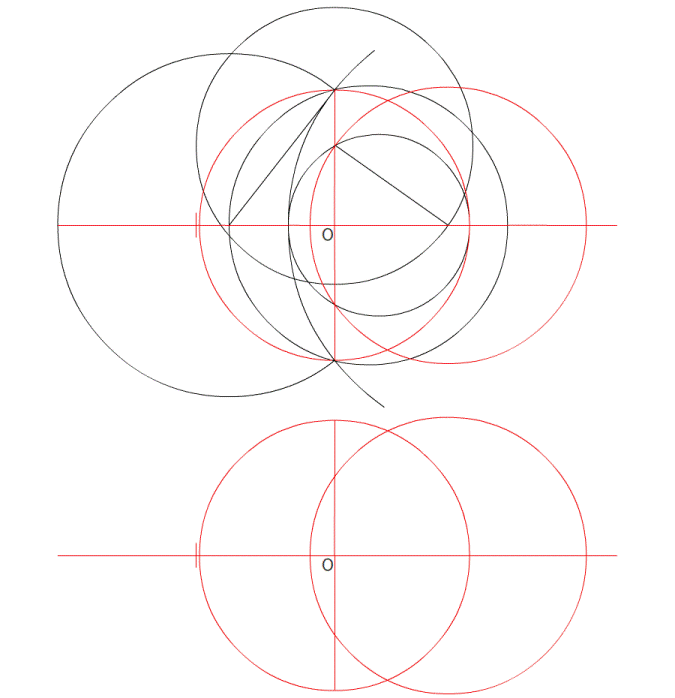 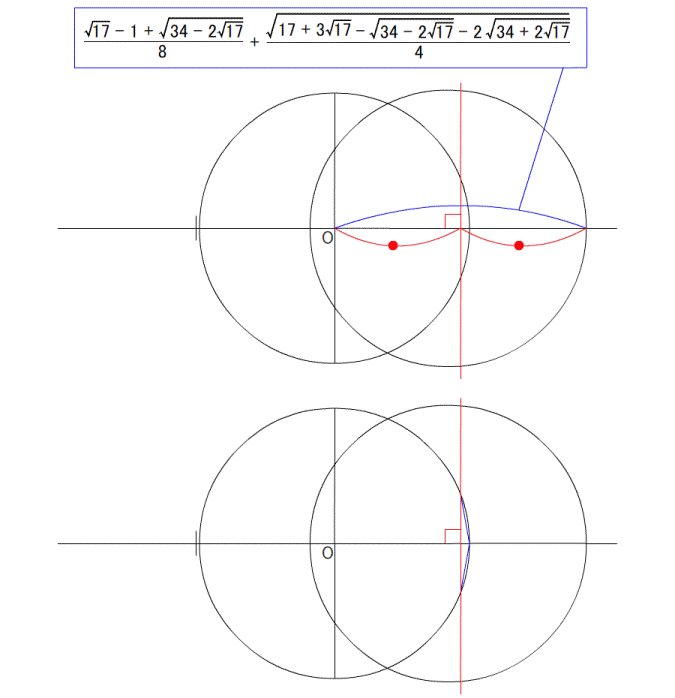 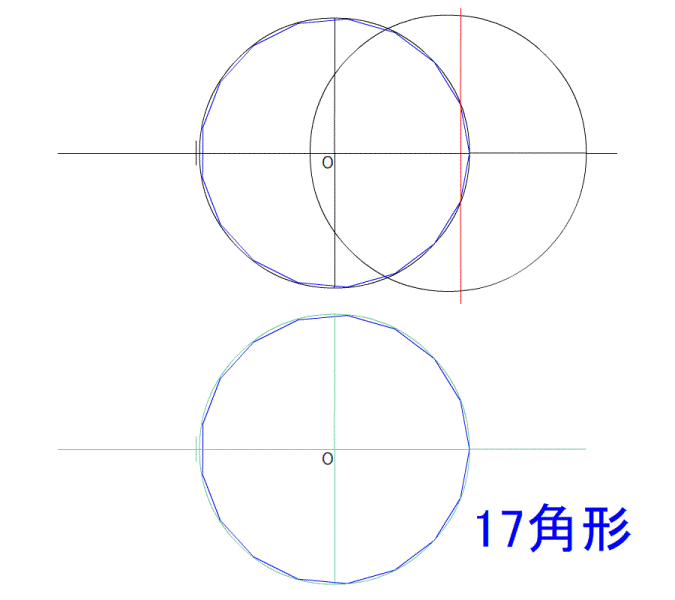 7つ目の作図は、計算に使うだけで作図自体には使いません。 まあ、だれも気にしていないと思いますが。 この発見は、正257角形 と 正65537角形 の作図可能も同時に導きました。 後に、正65537角形の作図につかう計算を200ページを越す論文に仕上げたのが、 ドイツの数学者ヘルメスであり、10年の歳月をかけたそうです。 ただ、作図はさすがにしなかったようです。 それは当然で、作図しようものなら、半径100メートルでも、一辺が9.6ミリしかなく、 それはどうみても 丸 であることでしょう。 この17や、255、65537などの数字はフェルマー素数という数なのですが・・・ どうやら誰も起きていないので、ここらで 『正17角形』 はおしまいです。 ご清聴、ありがとうございました。 zzz…。 ---------- 【おまけ話】 この式を思いついた19歳のガウスはこう思ったそうです。 『そうだ! 数学者になろう!』 ・・・お後が宜しい様で。 ---------- お気に入りの記事を「いいね!」で応援しよう
[【数学】] カテゴリの最新記事
|