shinの　じゅく日誌

角度が０°、９０°、１８０°、２７０°のときの三角比の値も

単位円を使って求めることができます。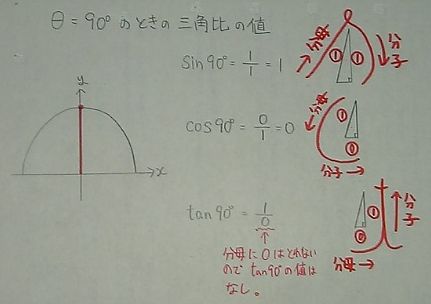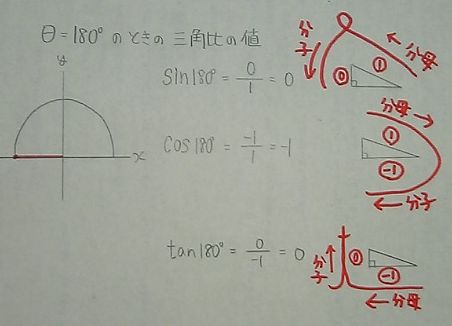









図を描いて求めていけば、最初はぎこちなくても

正確に、速く求められるようになる。

問題を解くときに、必ず小さくていいから

単位円を描いて解いていくべきだと思う。


さて次に、三角比の不等式（三角不等式）の問題を説明していきたいのですが

僕は単位円だけでは解かないようにしている。

三角比を関数にして、グラフ化したものを使う。（これを三角関数という）

一応、高２で習うところだけど、学校によってはかなりの割合で

この三角関数を習っていると思う。

三角不等式の問題は、単位円＋三角関数のグラフ　のセットで

解いたほうがいいと思っている。

なぜなら三角関数のグラフは

角度の変化により、三角比の値がどのように変わるのかが

ひと目見て分かるので便利だからだ。


今回はsin(サイン）、cos（コサイン）、tan（タンジェント）の

グラフを描いておきたい。

なお、tan(タンジェント）のグラフは角度が９０°、２７０°の前後を

注意して欲しい。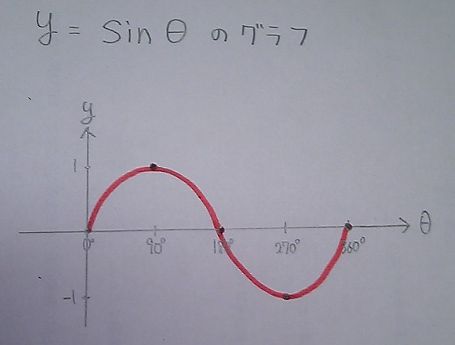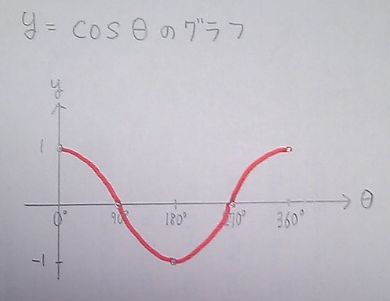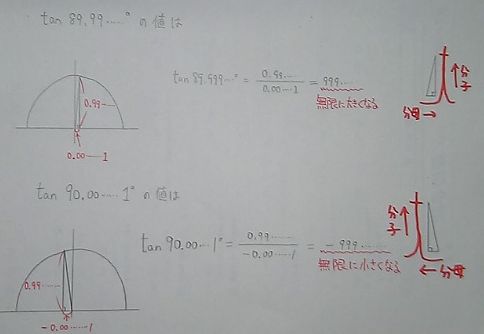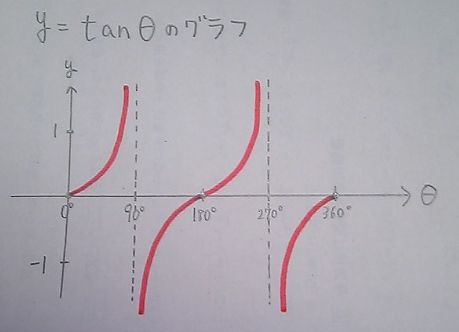










次回はこのグラフを使って、三角不等式の問題を解きます。