カスティール・アミスの雑記帳

問：Σ(k=1→40000) 1/√kの整数部分を求めよ。

コメント：この問題を数字で眺めても答えはでない。
数列の和を求める公式もないし、計算するとなると途方もない。
そこで考えてほしい。y＝1/√xを考えた場合、上の和の式は
図形的に何を表しているだろうか。こういう発想になったとき、
この問題は簡単に解けることに気がつく。これは積分の問題なのだと。
その時の感動はとても大きく、だからこの問題を紹介しようと思った。

解法：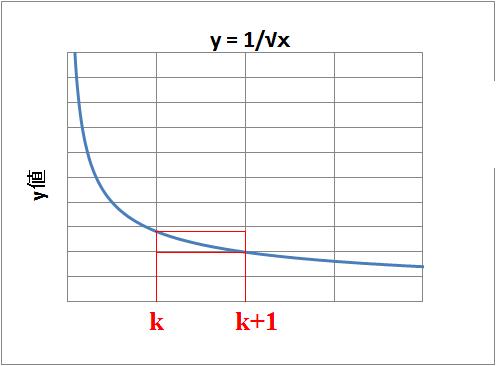


y＝f(x)=1/√xを考える。今、任意の整数kを用いて、
座標Ak(k,f(k)),Bk(k,f(k+1)),Ck(k+1,f(k+1)),Dk(k+1,f(k)),
Pk(k,0),Qk(k+1,0)を定義する。このとき、長方形
AkPkQkBkの面積をRk、CkPkQkDkの面積をSkとすると下記(1)式が成り立つ。

Sk < ∫(k→k＋1)1/√xdx < Rk
1/√(k+1) < ∫(k→k＋1)1/√xdx < 1/√k…(1)

（A)∫(k→k＋1)1/√xdx < 1/√kについて考える。

各kごとに積算していくと、

Σ(k=1→39999)∫(k→k＋1)1/√xdx < Σ(k=1→39999)1/√k
⇔∫(1→40000)1/√xdx < Σ(k=1→39999)1/√k
⇔∫(1→40000)1/√xdx < Σ(k=1→40000)1/√k - 1/√40000
⇔∫(1→40000)1/√xdx＋1/200 < Σ(k=1→40000)1/√k

よって定積分を行うと、
2*(√40000-√1)＋1/200 < Σ(k=1→40000)1/√k
⇔398＋1/200 < Σ(k=1→40000)1/√k…(2)

（B)1/√(k+1) < ∫(k→k＋1)1/√xdxについて考える。

各kごとに積算していくと

Σ(k=1→39999)1/√(k+1) < Σ(k=1→39999)∫(k→k＋1)1/√xdx
⇔Σ(k=1→39999)1/√(k+1) < ∫(1→40000)1/√xdx
⇔-1+Σ(k=1→40000)1/√k <∫(1→40000)1/√xdx

よって定積分を行うと

-1+Σ(k=1→40000)1/√k < 398
Σ(k=1→40000)1/√k < 399…(3)

(2)、(3)より398＋1/200 < Σ(k=1→40000)1/√k < 399
なのでその整数部分は398となる。